## Clase 8 ### Rotaciones  #### Puntos de vista activo y pasivo de las transformaciones de coordenadas Cualquier transformación aplicada sobre los puntos del espacio se puede pensar de dos formas diferentes: como un cambio del punto original por un nuevo punto (transformación activa) o como un cambio de las coordenadas del punto original por un nuevo sistema de coordenadas del mismo punto (transformación pasiva).  En el caso del espacio euclídeo tridimensional, los puntos se representan con vectores $\vec r$. Si nos limitamos a considerar transformaciones lineales, estas se pueden representar como una matriz. El punto de vista activo implica que la matriz se usa para transformar un vector $\vec r$ en otro vector $\vec r'$, según $\vec r'=M.\vec r$ (activo) El punto de vista pasivo implica que la matriz cambia las coordenadas $(\vec r)=(x,y,z)$ del vector $\vec r$ por otras coordenadas $(\vec r)'=(x',y',z')$ del mismo vector en otro sistema de coordenadas $(\vec r)'=M.(\vec r)$ (pasivo) #### Grupo de tranformaciones Las transformaciones lineales en espacio euclídeo cumplen la propiedad de ser un grupo, es decir que satisfacen las tres condiciones siguientes * Para cualquier transformación $M$ existe la tranformación inversa $M^{-1}$ que cumple $M^{-1}.\vec r'=\underbrace{M^{-1}.M}_I.\vec r=\vec r$ * La identidad es una transformación $I.\vec r=\vec r$ * Dadas dos transformaciones $M_1$ y $M_2$, la aplicación sucesiva $M_2.M_1$ también es una transformación $M_2.\vec r'=M_2.M_1.\vec r=\underbrace{(M_2.M_1)}_{M}.\vec r$ Cualquier subconjunto de transformaciones del espacio euclídeo que cumpla las tres condiciones de arriba es un grupo. Esta idea es importante porque las simetrías de un sistema físico son un grupo, dado que * Si una transformación es una simetría, la inversa también lo es. * La identidad siempre es una simetría. * La aplicación sucesiva de dos simetrías es una simetría. Entonces una condición para que un dado conjunto de transformaciones sea una simetría de un sistema físico, es que ese conjunto forme un grupo. #### Grupo ortogonal Una condición que cumplen las rotaciones es que dejan invariante el módulo del vector. Es decir que si definimos $\vec r'=R.\vec r$ Se cumple que $|\vec r'|=|\vec r|$ Ahora bien, dado que $|\vec r|=\sqrt{\vec r.\vec r}$ Podemos re-expresar la condición de invarianza como $\vec r'.\vec r'=|\vec r'|^2=|\vec r|^2=\vec r.\vec r$ Para poder expresar esta condición en términos de matrices, recordemos que los vectores son matrices columna, por lo que podemos escribir $\vec r'.\vec r'={\vec r'}^t.\vec r'=(x',y',z').\left(\begin{array}{c}x'\\y'\\z'\end{array}\right)$ Si ahora usamos que $\vec r'=R.\vec r$ tenemos ${\vec r'}^t.\vec r'=(R.\vec r)^t.(R.\vec r)={\vec r}^t.\underbrace{(R^t.R)}_I.\vec r=\vec r^t.\vec r$ Por lo tanto toda rotacion debe cumplir que $R^t.R=I$ O en otras palabras $R^t=R^{-1}$ Esto quiere decir que cualquier rotación es una *matriz ortogonal*, lo que se expresa como $R\in O(d)$ siendo $O(d)$ el conjunto de todas las matrices ortogonales de dimension $d$. Podemos probar que $O(d)$ es un grupo, porque * Dado $R\in O(d)$, se cumple que $R^{-1}\in O(d)$. En efecto, escribimos $(R^{-1})^t.R^{-1}=(R^t)^t.R^t=R.R^t=(R^t.R)^t=I^t=I$ Donde en la penúltima igualdad usamos $R^t.R=I$ * La identidad es una matríz ortogona $I\in O(d)$ $I^t.I=I.I=I$ * Dadas dos matrices ortogonales $R_1\in O(d)$ y $R_2\in O(d)$, se cumple que la composiión también es ortogonal $R_2.R_1\in O(d)$. En efecto, si escribimos $(R_2.R_1)^t.(R_2.R_1)=I=R_1^t.(\underbrace{R_2^t.R_2}_I).R_1=R_1^t.R_1=I$ Por lo tanto el conjunto de matrices ortogonales $O(d)$ es un grupo. #### Tranformaciones propias e impropias Utilizando la propiedad definitoria de las matrices ortogonales, podemos escribir ${\sf Det}(R^t.R)={\sf Det}\,I=1$ Usando las propiedades de los determinantes (el determinante de un producto es el producto de los determinantes y el determinante de la transpuesta es igual al determinante de la matriz) tenemos que ${\sf Det}(R^t.R)={\sf Det}\,R^t\, {\sf Det}\, R=({\sf Det} R)^2$ Por lo que se debe cumplir que $({\sf Det} R)^2=1$ o en otras palabras ${\sf Det} R=\pm 1$ Por lo tanto, hay matrices ortogonales con ${\sf Det} R=1$ (transformaciones propias) y otras con ${\sf Det}R=-1$ (transformaciones impropias). Llamaremos a las primeras *rotaciones* (más adelante probaremos que en efecto lo son) y a las segundas *reflexiones*. Un ejemplo de reflexión es la transformación de paridad en $x$, en la cual transfomamos el vector $\vec r=(x,y,z)$ en un nuevo vector $\vec r'=(x',y',z')=(-x,y,z)$ $\vec r'=P_x.\vec r$ Recordando que los vectores son matrices columna, tenemos que $\left(\begin{array}{c}x'\\y'\\z'\end{array}\right)=P_x.\left(\begin{array}{c}x\\y\\z\end{array}\right)$ Por lo que vemos que podemos representar $P_x$ con la matriz $\left(\begin{array}{c}-x\\y\\z\end{array}\right)=\underbrace{\left(\begin{array}{ccc}-1&0&0\\0&1&0\\0&0&1\end{array}\right)}_{P_x}.\left(\begin{array}{c}x\\y\\z\end{array}\right)$ Es evidente de aquí que se cumple ${\sf Det}\,P_x=-1$ por lo que $P_x$ es una reflexión. Por otro lado, es fácil verificar que se trata en efecto de una transformación ortogonal, según $P_x^2=P_x.P_x=\left(\begin{array}{ccc}-1&0&0\\0&1&0\\0&0&1\end{array}\right).\left(\begin{array}{ccc}-1&0&0\\0&1&0\\0&0&1\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)=I$  Podemos definir paridades en los otros ejes $P_y$ (cambiarle el signo a $y$) y $P_z$ (cambiarle el signo a $z$). Estarán dadas por $P_y=\left(\begin{array}{ccc}1&0&0\\0&-1&0\\0&0&1\end{array}\right)$ $P_z=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&-1\end{array}\right)$ Nótese que cualquier producto binario $P_x.P_y$ o $P_y.P_z$ o $P_z.P_z$ (y sus permutaciones) tendrá determinante $1$, por lo que no será una reflexión. Es fácil ver que estos productos representan las tranformación que cambia el signo a la vez a dos ejes cartesianos. Se puede ver también que ese cambio de signo de dos ejes a la vez siempre se puede reproducir rotando el sistema de coordenadas, por lo que no es una reflexión sino una rotación. Por otro lado el producto triple $P_x.P_y.P.z$ tiene determinante $-1$ y representa la transformación que le cambia el signo a la vez a los tres ejes cartesianos. Es fácil ver mirando un dibujo que esta transformación no se puede reproducir rotando el sistema de coordenadas, por lo que es una genuina reflexión. ##### Grupo $SO(d)$ Un reflexion cualquiera ${\sf Det} \,R=-1$ se puede escribir en términos de una rotación $R'$ con ${\sf Det}\, R'=1$ según $R=P_x.R'$. Para demostrarlo aprovechamos el hecho de que $P_x^2=I$ para escribir $-1={\sf Det}\,R={\sf Det}(P_x.P_x.R)={\sf Det}(P_x){\sf Det}(P_x.R)=-{\sf Det}(P_x.R)$ De donde sacamos que ${\sf Det}(\underbrace{P_x.R}_{R'})=1$ Por lo tanto podemos escribir $R=P_x.R'$ Esto significa que para estudiar las matrices ortogonales (rotaciones y reflexiones) $R \in O(d)$ podemos concentrarnos en las que tienen determinante $1$ (rotaciones). Estas últimas se conocen como *matrices especiales* y forman el conjunto $SO(d)$ > Ejercicio: probar que $SO(d)$ es un grupo, verificando que se cumplen las tres propiedades antes mencionadas. #### Descomposición de las rotaciones ##### Teorema de Euler Hasta ahora, hemos probado que toda rotación es un elemento de $O(d)$, pero que no todo elemento de $O(d)$ es una rotación, dado que ese conjunto también contiene a las reflexiones. Ahora bien, si nos limitamos a $SO(d)$, compuesto por las matrices ortogonales y especiales, que antes llamamos también transformaciones propias ¿será correcto decir que todas ellas son rotaciones? Además de no cambiar el módulo de los vectores, una rotación cualquiera se realiza *alrededor de un eje*, por lo que es correcto decir que deja invariante una dirección. Por lo tanto debe existir un vector $\check n$ tal que $R.\check n=\check n$ como se ve en el siguiente dibujo  Vamos a probar que tal vector existe para todas las matrices de $SO(d)$. Una matriz cualquiera cumple que $\left(R-I\right).R^t=I-R^t$ Tomando a ambos lados el determinante tenemos ${\sf Det}\,\left(\left(R-I\right).R^t\right)={\sf Det}\,\left(I-R^t\right)$ Usando propiedades de los determinantes tenemos ${\sf Det}\,\left(R-I\right)\,{\sf Det}\,R^{-1}={\sf Det}\,\left(I-R^t\right)$ Pero dado que ${\sf Det}\,R=1$ entonces ${\sf Det}\,\left(R-I\right)=\,{\sf Det}\,\left((I-R)^t\right)={\sf Det}\,\left(I-R\right)$ con lo que podemos escribir ${\sf Det}\,\left(R-I\right)=(-1)^d\,{\sf Det}\,\left(R-I\right)$ Donde hemos usado propiedades de los determinantes. Para $d$ impar (en nuestro caso $d=3$) esto implica ${\sf Det}\,\left(R-I\right)=-{\sf Det}\,\left(R-I\right)$ o tanto se cumple que ${\sf Det}\,\left(R-I\right)=0$ En otras palabras la matriz $R-I$ es singular, por lo que debe existir un vector $\check n$ tal que $\left(R-I\right).\check n=0$ o sea, un vector invariante $R.\check n=\check n$ ##### Rotación en torno a un eje  La pregunta ahora es ¿podemos escribir la matriz de rotación utilizando el eje de rotación $\check n$ y el ángulo $\theta$ de rotación alrededor de ese eje? Para hacerlo, necesitamos un sistema de ejes ortogonales en el que descomponer el vector $\vec r'$. Notando que $\check n$ es perpendicular a $\check n\times\vec r$ y que ambos son perpendiculares a $\check n\times(\check n\times\vec r)$, podemos construir un sistema de ejer perpendiculares en la dirección de esos tres vectores. Con esto, podemos dibujar el siguiente diagrama  Nótese que $|\vec r_\perp|=|\vec r'_\perp|=r\sin\varphi=|\check n\times \vec r|=|\check n \times(\check n\times\vec r)|$, con lo que es correcto dibujar todos estos vectores en el mismo círculo. Que nos permite descomponer $\vec r'=a\,\check n+\underbrace{b\,\left( {\check n\times\check r} \right)+c\,\check n\times\left({\check n\times\check r} \right)}_{\vec r'_\perp}$ donde claramente del dibujo se ve $a= \vec r.\check n= \vec r'.\check n$ $b=\sin\theta$ $c=-\cos\theta$ Con lo que obtenemos que $\vec r'=(\vec r.\check n)\,\check n+\sin \theta\,\,\check n\times \vec r-\cos \theta\, \,\check n\times(\check n\times \vec r)$ usando $\vec A\times(\vec B\times \vec C)=\vec C (\vec A.\vec B)-\vec B(\vec A.\vec C)$ podemos reescribir esta fórmula como $\vec r'=(\vec r.\check n)\,\check n+\sin \theta\,\,\check n\times \vec r+\cos \theta\, \,(\vec r-\check n(\check n.\vec r))$ Particularizando para un rotación en torno al eje $z$, tenemos que $\check n=\check k$. Escribiendo $\vec r=x\,\check i+y\, \check j+z\,\check k$ nos queda $\vec r'=z\,\check k+\sin \theta\,\,(-x\check j+y \check i)+\cos \theta\, \,(\vec r-\check k z)=R_z.\vec r$ Agrupando en la dirección de cada versor podemos escribir $\vec r'=z\,\check k+(\cos \theta\, \,x +\sin \theta\, y)\check i + (-\sin\theta\, x+\cos\theta \,y)\check j$ por lo que tenemos que $\vec r'=\left(\begin{array}{c}\cos \theta\, \,x +\sin \theta\, y\\-\sin\theta\, x+\cos\theta \,y\\z\end{array}\right)=R_z.\left(\begin{array}{c}x\\ y\\z\end{array}\right)$ En términos de la matriz $R_z=\left(\begin{array}{ccc}\cos \theta&\sin\theta&0\\-\sin\theta&\cos\theta &0\\0&0&1\end{array}\right)$ Es fácil probar que ${\sf Det}\,R_z=\cos^2\theta+\sin^2\theta=1$ y tambien que $R_z^t\cdot R_z=I$. > Ejercicio: pruebe que para una rotación alrededor del eje $x$ tenemos > > $R_x=\left(\begin{array}{ccc}1&0&0\\0&\cos \theta&\sin\theta\\0&-\sin\theta&\cos\theta\end{array}\right)$ > > Mientras que para una rotación en torno al eje $y$ nos queda > > $R_y=\left(\begin{array}{ccc}\cos \theta&0&-\sin\theta\\0&1&0\\\sin\theta&0&\cos\theta \end{array}\right)$ > > Verifique que en ambos casos las matrices son ortogonales y su determinante vale $1$. > Ejercicio: escribiendo el vector $\check n$ como $\check n=(\cos\vartheta\sin\varphi, \sin\vartheta\sin\varphi,\cos\varphi)$ obtenga la matriz $R_{\check n}$ tal que > > $\vec r'=(\vec r.\check n)\,\check n+\sin \theta\,\,\check n\times \vec r+\cos \theta\, \,(\vec r-\check n(\check n.\vec r))=R_{\check n}.\vec r$ y verifique que ${\sf Det} R_{\check n}=1$ y que $R_{\check n}^t.R_{\check n}=I$. ##### Descomposición de las rotaciones y ángulos de Euler Una rotación cualquiera se puede descomponer en rotaciones alrededor de los tres ejes. Una manera elegante y útil de hacerlo son los ángulos de Euler, definidos como sigue: para ir del vector original al vector rotado 1. Primero se realiza una rotación en un ángulo $\theta$ alrededor del eje $z$. 2. Luego se rota un ángulo $\phi$ alrededor del eje $x'$ resultante de la rotación anterior. 3. Finalmente se rota un ángulo $\psi$ alrededor del eje $z''$ resultante de ambas rotaciones. 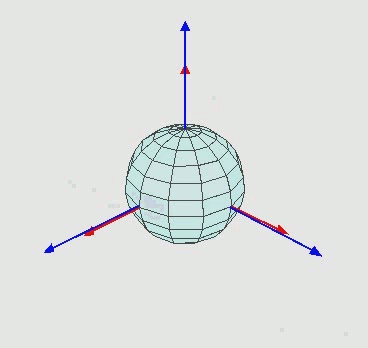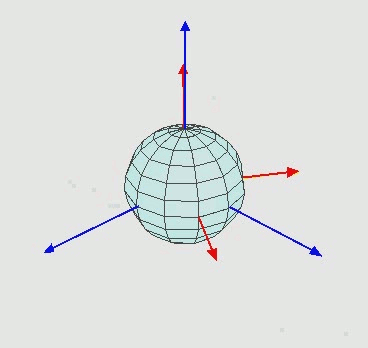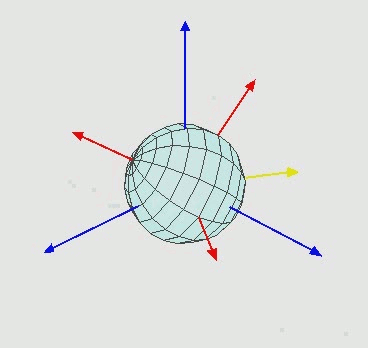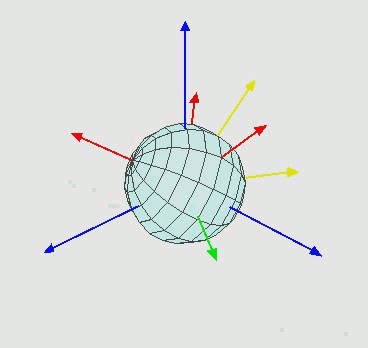La siguiente animacion aclara el proceso:  O en un dibujo estático  Esto implica que descomponemos la rotación $R$ en términos de tres rotaciones $R=R_{z''}.R_{x'}.R_z$ Usando la forma explícita de las rotaciones en cada eje, tenemos que $R=\left(\begin{array}{ccc}\cos \psi&\sin\psi&0\\-\sin\psi&\cos\psi &0\\0&0&1\end{array}\right).\left(\begin{array}{ccc}1&0&0\\0&\cos \phi&\sin\phi\\0&-\sin\phi&\cos\phi\end{array}\right).\left(\begin{array}{ccc}\cos \theta&\sin\theta&0\\-\sin\theta&\cos\theta &0\\0&0&1\end{array}\right)$ Es fácil convencerse que mediante este proceso se puede descomponer cualquier rotación. Los ángulos $\theta, \phi, \psi$ se conocen como *ángulos de Euler* de la rotación. Los valores de los ángulos son por supuesto diferentes de los de la convención anterior, pero también sirven para descomponer cualquier rotación. Como se muestra en este dibujo, esa convención es útil en aeronáutica:  #### Rotaciones infinitesimales y aceleración de Coriolis Imaginemos una rotación con un ángulo muy pequeño alrededor de un eje cualquiera. La podemos escribir como una matriz que está infinitesimalmente cerca de la identidad $R=I+\delta$ Donde los elementos de matriz de $\delta$ son muy pequeños, de tal modo que el cuadrado de cualquiera de ellos, o el producto de dos cualesquiera, es despreciable. Entonces podemos escribir el determiante como ${\sf Det }\,R=1+{\sf Tr}\,\delta+{\cal O}(\delta^2)$ > Ejercicio: pruebe la identidad anterior Por lo tanto la condición ${\sf Det }\,R=1$ implica que ${\sf Tr}\,\delta=0$. Por otro lado, las rotaciones son matrices ortogonales, es decir que cumplen que $R^t.R=I=(I+\delta)^t.(I+\delta)=(I+\delta^t).(I+\delta)$ Expandiendo la última expresión tenemos $(I+\delta^t).(I+\delta)=I+\delta^t+\delta+\underbrace{\delta^t.\delta}_{{\cal O}(\delta^2)}=I+\delta^t+\delta$ Por lo tanto la condición $R^t.R=I$ implica que $\delta^t+\delta=0$, o en otras palabras $\delta^t=-\delta$ Es decir que $\delta$ es una matriz antisimétrica. Una matriz antisimétrica general se puede escribir como $\left(\begin{array}{ccc}0&c&-b\\-c&0&a&\\b&-a&0\end{array}\right)= A\underbrace{\left(\begin{array}{ccc}0&0&0\\0&0&1&\\0&-1&0\end{array}\right)}_{t_1} +B\underbrace{\left(\begin{array}{ccc}0&0&-1\\0&0&0&\\1&0&0\end{array}\right)}_{t_2}+C\underbrace{\left(\begin{array}{ccc}0&1&0\\-1&0&0&\\0&0&0\end{array}\right)}_{t_3}$ En términos de las matrices $t_i$, que se llaman *generadores del grupo de rotaciones*. Por lo tanto tenemos que $R= I+A\,t_1+B\,t_2+C\, t_3$ Esto se resume diciendo que el grupo de rotaciones es un *grupo de Lie*. > Ejercicio; probar que > > $[t_1,t_2]=t_1.t_2-t_2.t_1= t_3$ > $[t_2,t_3]=t_2.t_3-t_3.t_2= t_1$ > $[t_3,t_1]=t_3.t_1-t_1.t_3= t_2$ > En general se puede probar que se cumple que $[t_i,t_j]=\epsilon_{ijk}t_k$ en lo que se conoces como *algebra de Lie del grupo de rotaciones*. Se puede verificar que las componentes de cada uno de estos generadores cumplen $(t_i)_{jk}=\epsilon_{ijk}$ Podríamos prenguntarnos cómo se relaciona esto con nuestra expresión general para las rotaciones con un ángulo $\theta$ alrededor de un eje $\check n$ $\vec r'=(\vec r.\check n)\,\check n+\sin \theta\,\,\check n\times \vec r+\cos \theta\, \,(\vec r-\check n(\check n.\vec r))$ Si imaginamos una rotación infinitesimal con un ángulo $d\theta$, podemos desarrollar $\sin \,d\theta=d\theta$ $\cos \,d\theta=1+{\cal O}(d\theta^2)$ con lo que reemplazando en la ecuación anterior tenemos $\vec r'=\vec r+d\theta\,\,\check n\times \vec r$ Escribiendo esta expresión en componentes, tenemos $r'_i=r_i+d\theta\,\epsilon_{ijk}n_jr_k=r_i-n_j(t_j)_{ik}r_k=\left(\delta_{ik}+d\theta\,n_j(t_j)_{ik}\right)r_k$ o en términos matriciales $\vec r'=(I+\underbrace{d\theta\,\check n.\vec t}_{\delta})\vec r$ donde $\vec t=(t_1,t_2,t_3)$ es un vector cuyas componentes son matrices (esto es simplemente una notación). Si definimos $\vec{d\theta}=\check n\,d\theta$ obtenemos que $d\vec r= \vec {d\theta}\times \vec r=\underbrace{(\vec{d\theta}.\vec t)}_\delta.\vec r=\delta.\vec r$ La primera igualdad toma una forma conocida cuando dividimos por $dt$ $\dot{\vec r}={\vec \omega}\times \vec r$ Podemos aplicar estas expresiones a la aceleración de Coriolis, como sigue: supongamos que las componentes de un vector cualquiera $\vec G$ en un sistema de coordenadas fijo respecto de las estrellas fijas se llaman $(\vec G)_S$, mientras que sus componentes en un sistema de coordenadas que rota solidario con la Tierra son $(\vec G)_T$. El origen de ambos sistemas está en el centro de la Tierra, y suponemos que inicialmente los ejes de ambnos sistemas están alineados. Tenemos entonces que, en el instante inicial $(\vec G)_{S}=(\vec G)_{T}$ Nótese que estamos usando el punto de vista pasivo para las rotaciones, es decir que consideramos que el vector es el mismo, y que el efecto de la rotación es darnos las componentes en un nuevo sistema de coordenadas que está rotado respecto del original. La notación $(\vec G)_S$ debe leerse *las componentes del vector $\vec G$ en el sistemas $S$ (y similarmente para $T$)*. Al dejar pasar un pequeño intervalo de tiempo $dt$, los sistemas han rotado un ángulo $d\Theta$, por lo que $(\vec G+d\vec G)_{S}=(I+\delta)(\vec G+d\vec G)_{T}=(I+\vec {d\Theta}.\vec t)(\vec G+d\vec G)_{T}$ De donde podemos escribir $(\vec G)_S+d(\vec G)_{S}=(\vec G)_{T}+d(\vec G)_{T}+(\vec {d\Theta}.\vec t).(\vec G)_{T}+\cdots$ o en otras palabras $d(\vec G)_{S}=d(\vec G)_{T}+\vec {d\Theta}\times(\vec G)_{T}$ donde el primer término representa el cambio intrínseco en las componentes del vector, mientras que el segundo se refiere al cambio debido a la rotación del sistema de coordenadas fijo a la Tierra. Dividiendo por $dt$ obtenemos $\frac{d(\vec G)_S}{dt}=\frac {d(\vec G)_T}{dt}+\vec \Omega\times(\vec G)_T$ Nótese que $d(\vec G)_T/dt\neq (d\vec G/dt)_T$ debido a la rotación del sistema $T$. Aplicando este resultado al vector posición $\vec G=\vec r$, tenemos $(\vec v)_S=\frac{d(\vec r)_S}{dt}=\frac {d(\vec r)_T}{dt}+\vec \Omega\times(\vec r)_T$ Nótese que $d(\vec r)_T/dt\neq (\vec v)_T$. Si ahora pensamos que $\vec G=\vec v$ podemos escribir $(\vec a)_S= \frac{d(\vec v)_S}{dt}= \frac {d}{dt}\left(\frac {d(\vec r)_T}{dt}+\vec \Omega\times(\vec r)_T\right)_S=\frac {d }{dt}\left(\frac {d(\vec r)_T}{dt}+\vec \Omega\times(\vec r)_T\right)_T+\vec\Omega\times\left(\frac {d(\vec r)_T}{dt}+\vec \Omega\times(\vec r)_T\right)_T$ reordenando tenemos $(\vec a)_S=\frac {d^2(\vec r)_T}{dt^2}+2\,\vec \Omega\times\frac {d(\vec r)_T }{dt}+\vec\Omega\times\left(\vec \Omega\times(\vec r)_T\right)$ El primer término es la aceleración en el sistema $T$, el segundo término nos da la *aceleración de Coriolis*, mientras que el tercero corresponde a la aceleración centrípeta. ## Clase 9 ### Cuerpo rígido  Supongamos que tenemos un sistema de $N$ partículas, El conjunto formado por las tres componentes de cada uno de los vectores posición $\vec r_a$ constituye un sistema de coordenadas generalizadas. A continuación vamos a contruir otro sistema de coordenadas generalizadas para describir su movimiento, como sigue: Tomamos tres partículas cualesquiera no colineales $a=1,2,3$. Estas partículas forman un triángulo. La posición de las tres partículas estará completamente determinada por la forma, posición y orientación del triángulo. * La forma del triángulo está dada por las longitudes de cada uno de sus lados $l_1,l_2,l_3$. * La posición del triángulo está dada por la posición de uno de sus vértices $\vec r_1$. * La orientación del triángulo es fijada por la dirección $\check u$ en el espacio en la que apunta uno de sus lados, y el ángulo $\alpha$ que forma el plano del triángulo con una dirección fija cualquiera. La posición de cualquier otra partícula $a>3$ del sistema estará dada por la distancias $l_{a1},l_{a2},l_{a3}$ que la separan de los tres vértices del tríangulo. Con esto, nuestro conjunto de coordenadas generalizadas está dado por $\vec r_1,\check u,\alpha, l_1,l_2,l_3$ y $l_{a1},l_{a2},l_{a3}$ para $a>3$. Son $3$ componentes de $\vec r_1$, tres angulos dados por los dos ángulos que determinan $\check u$ y el ángulo $\alpha$, y $3+3(N-3)=3N-6$ distancias. Comprobamos que es un total de $3N$ coordenadas. Un *cuerpo rígido* es un sistema de partículas tal que la distancia entre cualquier par de partículas es constante. Por lo tanto, las $3N-6$ distancias mencionadas más arriba no cambiarán con el tiempo, y podemos dejarlas fijas en nuestra descripción del cuerpo rígido. Esto puede involucrar alguna sutileza, ya que esas coordenadas genralizadas también tienen sus ecuaciones de movimiento, y deberíamos asegurarnos que cuando las dejamos fijas estas ecuaciones se están cumpliendo. Postpondremos esa discusión para más adelante. Como conclusión, un cuerpo rígido tiene seis grados de libertad, dados por la posición de una de sus partículas $\vec r_1$ (podría ser por ejemplo el centro de masas), los dos angulos del vector $\check u$ y un ángulo $\alpha$ adicional. Estos tres ángulos suelen reemplazare por los ánculos de Euler $\theta,\phi,\psi$ que forma un sistema de coordenadas unido al cuerpo respecto de un sistema de coordenadas fijo externo. #### Momento de inercia Supongamos que queremos escribir el momento de angular del cuerpo rígido $\vec L=m_a(\vec r_a\times \vec v_a)=m_a(\vec r_a\times (\vec \omega\times\vec r_a))$ Donde $a$ es el índice que corre entre todas las partículas del cuerpo, y estamos sumando sobre él. en la segunda igualdad hemos usado que $v_a=\omega\times \vec r_a$, es decir que estamos en un sistema de coordenadas que está en reposo respecto del centro de rotación del cuerpo, por lo que el único movimiento será el de rotación alrededor de un eje. Si usamos que para un producto vectorial triple $\vec A\times (\vec B\times \vec C)=\vec B(\vec A.\vec C)-\vec C(\vec A.\vec B)$ tenemos que $\vec L=m_a(\vec \omega \,\vec r_a^2-\vec r_a(\vec\omega.\vec r_a))$ Lo que en componentes se puede escribir como $L_i=m_a(\omega_i \,\vec r_a^2-r^a_i\omega_j r^a_j)$ Donde en el segundo término hay una suma sobre $j$. Para poder sacar factor común $\omega_j$ insertamos una $\delta_{ij}$ en el rimer término, y tenemos $L_i=m_a(\delta_{ij}\omega_j \,\vec r_a^2-r^a_i\omega_j r^a_j)=\underbrace{m_a(\delta_{ij} \,\vec r_a^2-r^a_i r^a_j)}_{{\cal I}_{ij}}\omega_j={\cal I}_{ij}\omega_j$ Las magnitudes ${\cal I}_{ij}$ forman una matriz $\cal I$ llamada *matriz momento de inercia*, que nos permite escribir $\vec L={\cal I}.\vec \omega$ Esto se puede hacer más explícito según $L_x={\cal I}_{xx} \omega_x+{\cal I}_{xy} \omega_y+{\cal I}_{xz} \omega_z$ $L_y={\cal I}_{yx} \omega_x+{\cal I}_{yy} \omega_y+{\cal I}_{yz} \omega_z$ $L_z={\cal I}_{zx} \omega_x+{\cal I}_{zy} \omega_y+{\cal I}_{zz} \omega_z$ Nótese que la matriz ${\cal I}$ es una matriz simétrica, de acuerdo a su definición. ¿Qué es esta matriz? Hasta ahora hemos aprendido en los cursos básicos de física que existen los vectores, como por ejemplo el momento angular $\vec L$. Estos vectores estan definidos una terna de números $\vec L=(L_x, L_y, L_z)$, pero además de eso satisfacen una propiedad fundamental que es su regla de transformación frente a rotaciones $\vec L'=R.\vec L$ O en componentes $L_i=R_{ij}L_j$ Una terna de números que se transforma de esa manera frente a las rotacioens se llama *vector contravariante*. Existen también los *vectores covariantes* que transforman con la matriz transpuesta, como por ejemplo $\partial_i'=R_{ji}\partial_j$ > Ejercicio: probar la regla de transformación anterior Uno podría preguntarse entoces ¿cómo se tansforman la matriz de $3\times 3$ que constituye el momento de inercia? Para ver eso, aplicamos una rotación al momento angular, obteniendo $R.\vec L=R.{\cal I}.\vec \omega$ En el miembro derecho podemos insertar la identidad escrita como $I=R^t.R$ y nos queda $R.\vec L=R.{\cal I}.(R^t.R).\vec \omega=\underbrace{(R.{\cal I}.R^t)}_{{\cal I}'}.\underbrace{R.\vec \omega}_{\vec \omega'}$ Con lo que obtenemos $\vec L'={{\cal I}'}.\vec \omega'$ Esto implica que el momento de inercia transforma de acuerdo a ${\cal I}'=R.{\cal I}.R^t$ o en componentes ${\cal I'}_{ij}=R_{ik}{\cal I}_{kl}R_{jl}=R_{ik}R_{jl}{\cal I}_{kl}$ En otras palabras, el momento de inercia es un *tensor de dos índices contravariante*. Existen tendsores de más índices contravariantes, definidos según la regla de transformación $T_{ijk\dots}'=R_{il}R_{js}R_{kt}\dots T_{lst\dots}$ Un ejemplo es el *tensor de Levi-Civita* dado por $\epsilon_{ijk}$. Ahora bien, si tomamos el producto de las componentes de dos vectores cualesquiera $\vec v$ y $\vec w$, y aplicamos una rotación, tenemos que $v'_iw'_j=R_{ik}v_kR_{jl}w_l=R_{ik}R_{jl}v_kw_l$ Lo que nos permite definir un objeto $\vec v\otimes\vec w$ cuyas componentes son $(\vec v\otimes\vec w)_{ij}=v_iw_j$ que forma un tensor de dos índices contravariante. Ese objeto nos sirve para re-escribir la fórmula para el momento de inercia como ${\cal I}=m_a\left(r_a^2I-\vec r_a\otimes \vec r_a\right)$ Ahora bien, para entender qué relación tiene este *tensor momento de inercia* con los objetos de los que hablamos en los cursos elementales de física, escribimos la energía cinética como $K=\frac 12 m_a\vec v_a^2$ $K=\frac 12 m_a \vec v_a.(\vec \omega \times \vec r_a)= \frac 12 \underbrace{m_a( \vec r_a\times \vec v_a)}_{\vec L}. \vec \omega=\frac 12 \vec L^t.\vec \omega=\frac 12 ({\cal I}.\omega)^t.\omega=\frac 12 \vec \omega^t.{\cal I}.\vec \omega$ Donde en la segunda igualdad hicimos una rotación cíclica del producto mixto. Escribiendo la velocidad angular como $\vec \omega = \omega\, \check n$, donde $\check n$ es la dirrección del eje de rotaciuón, tenemos que $K=\frac 12 \underbrace{(\check n^t.{\cal I}.\check n)}_{{\cal I}_{\check n}}\,\omega^2=\frac 12 {\cal I}_{\check n} \omega^2$ Donde hemos definido el *momento de inercia alrededor de un eje $\check n$*. ${\cal I}_{\check n}=\check n^t.{\cal I}.\check n$ En componentes tenemos ${\cal I}_{\check n}=n_i{\cal I}_{ij}n_j=n_im_a\left(r_a^2\delta_{ij}-r^a_ir^a_j\right)n_j=m_a\left(r_a^2\delta_{ij}n_in_j-r^a_ir^a_jn_in_j\right)=m_a\left(r_a^2-(\vec r^a.\check n)^2\right)$ Lo que usando el teorema de Pitágoras nos permite escribir ${\cal I}_{\check n}=m_a\left(r_a^2-(\vec r^a.\check n)^2\right)=m_a\rho_a^2$ ##### Teorema de Steiner Esta forma del momento de inercia facilita la prueba del Teorema de Steiner. En efecto, si tenemos ${\cal I}=m_a\left(r_a^2I-r_a\otimes r_a\right)$ Donde $\vec r_a=\vec R+\vec r'_a$ con $\vec R$ la posición del centro de masas y $\vec r'_a$ la posición de la partícula $a$ en el sistema centro de masas, podemos poner ${\cal I}=m_a \left((\vec R+\vec r'_a)^2I-(\vec R+\vec r'_a)\otimes(\vec R+\vec r'_a)\right)=m_a({r'}_a^2I-\vec r'_a\otimes \vec r'_a)+m_a(R^2I-\vec R\otimes \vec R)+\cdots$ > Ejercicio: escriba explítitamente los términos omitidos en la expresión de earriba y prueba que se anulan usando que en el sistema centro de masas $m_a\vec r'_a=0$. Con esto nos quedea ${\cal I}={\cal I}'+M(R^2I-\vec R\otimes \vec R)$ Donde $M=\sum_a m_a$. Si usamos esta expresión en el momento de inercia alrededor de un eje ${\cal I}_{\check n}={\check n}^t.{\cal I}.{\check n}$, obtenemos ${\cal I}_{\check n}={\cal I}'_{\check n}+M\Delta^2$ con $\Delta^2 = R^2-(R.\check n)^2$. ##### Ejes principales Para entender qué son los ejes principales de un cuerpo rígido, escribimos la *ecuación de autovalores* ${\cal I}.\vec w ={\cal J} \vec w$ La solución de esta ecuación viene dada por un vector $\vec w$ que se llama *autovector* de la matrix ${\cal I}$, y por un escalar ${\cal J}$ que se llama *autovalor* de la matrix ${\cal I}$. Por supuesto puede haber varias soluciones ${\cal J}_i, \vec w_i$ ${\cal I}.\vec w_i ={\cal J}_i \vec w_i$ Vamos a probar que esta soluciones son reales. Para esto, multiplicamos escalarmente por $\vec w_i^*$ y la fórmula se escribe $({\vec w^*}_j)^t.{\cal I}.\vec w_i ={\cal J}_i \,({\vec w^*}_j)^t.\vec w_i$ cambiando $i$ por $j$ $({\vec w^*}_i)^t.{\cal I}.\vec w_j ={\cal J}_j \,({\vec w^*}_i)^t.\vec w_j$ conjugando $({\vec w}_i)^t.{\cal I}^*.\vec w_j^* ={\cal J}_j^* \,({\vec w}_i)^t.\vec w_j^*$ transponiendo $(({\vec w}_i)^t.{\cal I}^*.\vec w_j^*)^t =({\cal J}_j^* \,({\vec w}_i)^t.\vec w_j^*)^t$ $({\vec w^*}_j)^t.{\cal I}^\dagger.\vec w_i ={\cal J}_j^* \,({\vec w}^*_j)^t.\vec w_i$ y usando el hecho de que ${\cal I}$ es una matriz real y simétrica $({\vec w^*}_j)^t.{\cal I}.\vec w_i ={\cal J}_j^* \,({\vec w}^*_j)^t.\vec w_i$ restando esto de la ecuación con la que comenzamos $0=({\cal J}_i-{\cal J}_j^*) \,({\vec w}^*_j)^t.\vec w_i$ Si elegimos el caso $i=j$ tenemosque $0=({\cal J}_i-{\cal J}_i^*) \,({\vec w}^*_i)^t.\vec w_i$ Nótese que $({\vec w}^*_i)^t.\vec w_i=w_x^*w_x+w_y^*w_y+w_z^*w_z=|w_x|^2+|w_y|^2+|w_z|^2>0$, por lo que esta ecuación implica que ${\cal J}_i={\cal J}_i^*$. En otras palabras ${\cal J}_i$ es real, y luego por la primera ecuación $\vec w_i$ son reales. Si en cambio elegimos $i\neq j$ $0=({\cal J}_i-{\cal J}_j) \,({\vec w}_j)^t.\vec w_i$ Con esto tenemos que * Si ${\cal J}_i\neq{\cal J}_j$ implica $({\vec w}_j)^t.\vec w_i=\vec w_j.\vec w_i=0$ por lo tanto $\vec w_i\perp \vec w_j$ * Si ${\cal J}_i={\cal J}_j$ se pueden elegir $\vec w_i$ y $\vec w_j$ que son solución de la ecuación y que son perpendiculares. > Ejercicio: probar la segunda afirmación Con esto tenemos que la ecuación de autovalores tiene como solución tres vectores mutuamente perpendiculares. Estos vectores nos permiten escribir el momento de inercia según ${\cal I}={\cal J}_i(\vec w_i\otimes\vec w_i)$ Para probar que esta descomposición es correcta, usamos su forma en componentes ${\cal I}_{kl}={\cal J}_i(\vec w_i)_k(\vec w_i)_l$ y la insertamos en la ecuación de autovalores, obteniendo ${\cal I}_{kl}(\vec w_j)_l={\cal J}_i(\vec w_i)_k(\vec w_i)_l(\vec w_j)_l={\cal J}_i(\vec w_i)_k\, (\vec w_i).(\vec w_j)={\cal J}_i(\vec w_i)_k\delta_{ij}={\cal J}_j(\vec w_j)_k$ Lo que muestra que, en efecto, la descomposición que hemos escrito para ${\cal I}$ cumple la ecuación de autovalores. Esta descomposición es útil si elegimos nuestro sistema de coordenadas en las direcciones de nuestros tres vectores $\vec w_i$ mutuamente ortogonales. Esto nos permite escribir $\vec w_1=|\vec w_1|(1,0,0)$, $\vec w_1=|\vec w_2|(0,1,0)$ y $\vec w_3=|\vec w_3|(0,0,1)$ y obtener $\cal I =\left(\begin{array}{ccc}{\cal J}_1&0&0\\0&{\cal J}_2&0\\0&0&{\cal J}_3\end{array}\right)$ En términos de los *momentos de inercia principales ${\cal J}_1,{\cal J}_2,{\cal J}_3$* a los largo de los *ejes principales* $\vec w_1, \vec w_2, \vec w_3$. Para obtener los valores de estos tres momentos principales, tenemos que resolver ${\cal I}.\vec w={\cal J}\vec w$ $\left({\cal I}-{\cal J}I\right).\vec w=0$ ${\sf Det}({\cal I}-{\cal J}I)=0$ En términos de ellos, podemos escribir $L_1={\cal J}_1\omega_1$ $L_2={\cal J}_2\omega_2$ $L_3={\cal J}_3\omega_3$ Con lo que tenemos $K=\frac 12 \vec \omega^t.{\cal I}.\vec \omega =\frac 12 \left({\cal J}_1\omega_1^2+{\cal J}_2\omega_2^2+{\cal J}_3\omega_3^2\right)=\frac1{2{\cal J}_1}L_1^2+\frac1{2{\cal J}_2}L_2^2+\frac1{2{\cal J}_3}L_3^2$ Como vemos, las expresiones en términos de los momentos principales de inercia son mucho más simples y no incluyen matrices, por lo que serán útiles para escribir las ecuaciones de movimiento de un cuerpo rígido. ## Clase 10  ##### Ecuaciones de Euler Con lo que aprendimos tenemos entonces una expresión para el lagrangiano de un cuerpo rígido, dada por $L=\frac 12 M\dot r_1^2+\frac 12\vec \omega^t.{\cal I}.\vec \omega-V(\vec r_1,\theta,\psi,\phi)$ De aquí obtenemos la ecuación que nos relaciona la derivada del momento angular con el torque, segun $\frac {d\vec L}{dt}=\vec \tau$ En el sistema de coordenadas que está en reposo, esa ecuación se lee para cada componente como $\left(\frac {d\vec L}{dt}\right)_S=(\vec \tau)_S$ En cambio, en el sistema de coordenada que gira junto con el cuerpo, esa ecuación toma otra forma, incluyendo la contribución que vimos más arriba originada en la rotación del sistema de coordenadas. En otras palabras, cada componente cumple $\left(\frac{d\vec L}{dt}\right)_B+(\vec \omega\times\vec L)_B=(\vec \tau)_B$ Si recordamos que $\vec L={\cal I}.\vec \omega$ entonces $\left(\frac{d({\cal I}.\vec \omega)}{dt}\right)_B+(\vec \omega\times({\cal I}.\vec \omega))_B=(\vec \tau)_B$ o en componentes ${\cal I}_{ij}\frac{d \omega_j}{dt}+\epsilon_{ijk}\omega_j {\cal I}_{kl}\omega_l= \tau_i$ Lo que en las direcciones de los ejes principales donde ${\cal I}_{ij}={\cal J}^{(j)}\delta_{ij}$ se lee ${\cal J}^{(j)}\delta_{ij}\frac{d \omega_j}{dt}+\epsilon_{ijk}\omega_j {\cal J}^{(k)}\delta_{kl}\omega_l= \tau_i$ mas explícitamente ${\cal J}^{(i)}\frac{d \omega_i}{dt}+\epsilon_{ijk}\omega_j {\cal J}^{(k)} \omega_k= \tau_i$ o bien ${\cal J}_x\frac{d \omega_x}{dt}+ \left({\cal J_z} - {\cal J_y}\right) \omega_y\omega_z=\tau_x$ ${\cal J}_y\frac{d \omega_y}{dt}+ \left({\cal J_z} - {\cal J_x}\right) \omega_x\omega_z=\tau_y$ ${\cal J}_z\frac{d \omega_z}{dt}+ \left({\cal J_x} - {\cal J_y}\right) \omega_x\omega_y=\tau_z$ Estas ecuaciones se llaman *ecuaciones de Euler* y determinan completamente el movimiento de un cuerpo rígido sometido a un torque. ##### Cuerpo rígido libre e inestabilidad de Dzhanibekov En el caso del cuerpo rígido libre $\vec \tau =0$, las ecuaciones de Euler quedan escritas como ${\cal J}_x\frac{d \omega_x}{dt}+ \left({\cal J_z} - {\cal J_y}\right) \omega_y\omega_z=0$ ${\cal J}_y\frac{d \omega_y}{dt}+ \left({\cal J_z} - {\cal J_x}\right) \omega_x\omega_z=0$ ${\cal J}_z\frac{d \omega_z}{dt}+ \left({\cal J_x} - {\cal J_y}\right) \omega_x\omega_y=0$ Es fácil ver que tienen una solución trivial con $\omega_x=\omega_x^0$ constante y $\omega_y=\omega_z=0$. Es decir que el cuerpo rígido gira alrededor de uno de sus ejes principales con velocidad angular constante. Una pregunta natural es qué pasa si perturbamos ese movimiento ligeramente, es decir si escribimos $\omega_x=\omega_x^0+\delta\omega_x$ $\omega_y=\delta \omega_y$ $\omega_z=\delta \omega_z$ con $\delta \omega_x, \delta\omega_y$ y $\delta\omega_z$ magnitudes pequeñas. Entonces las ecuaciones de Euler quedan ${\cal J}_x\frac{d \delta\omega_x}{dt}+ \left({\cal J_z} - {\cal J_y}\right) \delta\omega_y\delta\omega_z=0$ ${\cal J}_y\frac{d \delta\omega_y}{dt}+ \left({\cal J_z} - {\cal J_x}\right) (\omega_x^0+\delta\omega_x)\delta\omega_z=0$ ${\cal J}_z\frac{d \delta\omega_z}{dt}+ \left({\cal J_x} - {\cal J_y}\right) (\omega_x^0+\delta\omega_x)\delta\omega_y=0$ Expandiendo estas ecuaciones y tirando cualquier cosa que sea cuadrática en $\delta \omega_x, \delta\omega_y$ y $\delta\omega_z$ tenemos $\frac{d \delta\omega_x}{dt} =0$ ${\cal J}_y\frac{d \delta\omega_y}{dt}+ \left({\cal J_z} - {\cal J_x}\right) \omega_x^0\,\delta\omega_z=0$ ${\cal J}_z\frac{d \delta\omega_z}{dt}+ \left({\cal J_x} - {\cal J_y}\right) \omega_x^0\,\delta\omega_y=0$ Para resolver este sistema, podemos tomar una derivada temporal adicional en la segunda ecuación ${\cal J}_y\frac{d^2 \delta\omega_y}{dt^2}+ \left({\cal J_z} - {\cal J_x}\right) \omega_x^0\,\frac{d\delta\omega_z}{dt}=0$ y reemplazar aquí la tercera ecuación $\frac{d \delta\omega_z}{dt}=- \frac{{\cal J_x} - {\cal J_y}}{{\cal J}_z} \omega_x^0\,\delta\omega_y$ obteniendo $\frac{d^2 \delta\omega_y}{dt^2}+ \underbrace{\frac{\left({\cal J_x} - {\cal J_z}\right)\left({\cal J_x} - {\cal J_y}\right)}{{\cal J}_y{\cal J}_z} (\omega_x^0)^2}_{\nu^2}\,\delta\omega_y=0$ Donde hemos supuesto que el factor sobre la llave es positivo. Con esto nos queda una ecuación para $\delta\omega_y$ dada por $\frac{d^2 \delta\omega_y}{dt^2}+ {\nu^2}\,\delta\omega_y=0$ Esta es la ecuación de un oscilador armónico, con la solución inmediata $\delta\omega_y=A\,\cos\left(\nu \,t+\varphi\right)$ > Ejercicio: obtenga la solución para $\delta\omega_z$ Es decir que la perturbación hara que la dirección de la velocidad angular oscile alrededor del eje original de rotación $x$. Pero ¿qué pasa si el factor sobre la llave es negativo? En ese caso escribimos $\frac{d^2 \delta\omega_y}{dt^2}+ \underbrace{\frac{\left({\cal J_x} - {\cal J_z}\right)\left({\cal J_x} - {\cal J_y}\right)}{{\cal J}_y{\cal J}_z} (\omega_x^0)^2}_{-\tilde\nu^2}\,\delta\omega_y=0$ Con lo que la solución es $\delta\omega_y=A_+e^{+\tilde\nu \,t}+A_-e^{-\tilde\nu \,t}$ > Ejercicio: obtenga la solución para $\delta\omega_z$ Es decir que ahora la pequeña perturbación crecerá exponencialmnte hasta dejar de ser pequeña, la rotación del cuerpo rígido se desestabiliza cambiando de dirección.  Esto se conoce como efecto Dzhanibekov, por el cosmonauta ruso que lo filmó en la estación espacial Mir. ¿De que depende el signo de la magnitud sobre la llave? Claramente depende de la combinación $\left({\cal J_x} - {\cal J_z}\right)\left({\cal J_x} - {\cal J_y}\right)$ Nótese que esta combinación será positiva tanto cuando ${\cal J}_x$ sea el mayor de los momentos de inercia principales, como cuando sea el menor, y será negativa en cambio cuando ${\cal J}_x$ sea el momento de inercia intermedio. En otras palabras, la rotación de un cuerpo rígido es estable a lo largo del mayor o del menor de sus ejes principales, y es inestable alrededor del eje intermedio.  Este efecto se conoce también como *teorema de la raqueta* porque se hace evidente al arrojar al aire una raqueta de tenis. ##### Lagragiano para un cuerpo rígido: trompo Si queremos escribir el lagrangiano $L=K-V$ para un cuerpo rígido tenemos que escribir su energía cinética $K = \frac12{\cal J}_1\omega_1^2+\frac12{\cal J}_2\omega_2^2+\frac12{\cal J}_3\omega_3^2$ en términos de algún conjunto de coordenadas generalizadas, por ejemplo los ángulos de Euler  En el sistema del dibujo, podemos escribir la velocidad angular como una superposición de una rotación alrededor de cada uno de los ejes en los cuales definimos los ángulos de Euler, según $\vec\omega=\vec\omega_\psi+\vec\omega_\theta+\vec\omega_\phi$ donde $\vec\omega_\psi=\dot\psi\,\check k''$ $\vec\omega_\theta=\dot\theta\,\check i'$ $\vec\omega_\phi=\dot\phi\,\check k$ Ahora bien, en términos de los ejes principales del cuerpo, tendremos que uno de ellos apunta en la dirección $z''$, mientras que los otros dos apuntarán en las direcciones $x'$ e $y''$. Por lo tanto $\vec\omega=\dot\psi\,\check k''+\dot\theta\,\check i'+\dot\phi\,\check k$ Los tres ejes principales son $\check i'',\check j''$ $\omega_2=\vec \omega.\check i''=\dot\theta$ $\omega_3=\vec \omega.\check j''=\dot\phi\,\sin\theta$ $\omega_1=\vec \omega.\check k''=\dot\psi+\dot\phi\,\cos \theta$ Esto nos permite escribir para la energía cinética $K=\frac12{\cal J}_1(\dot\psi+\dot\phi\,\cos\theta)^2+\frac12{\cal J}_2\dot\theta^2+\frac12{\cal J}_3\sin^2\theta\,\dot \phi^2$ con lo que podemos obtener el lagrangiano en la forma $L=\frac12{\cal J}_1(\dot\psi+\dot\phi\,\cos\theta)^2+\frac12{\cal J}_2\dot\theta^2+\frac12{\cal J}_3\sin^2\theta\,\dot \phi^2-V(\theta,\phi, \psi)$ Si el trompo es simétrico entonces ${\cal J}_2={\cal J}_3$, con lo que la expresión se simplifica $L=\frac12{\cal J}_1(\dot\psi+\dot\phi\,\cos\theta)^2+\frac12{\cal J}_2\left(\dot\theta^2+\sin^2\theta\,\dot \phi^2\right)-mgl\,\cos\theta$ Donde hemos supuesto que la única energía potencial es la gravitatoria, y que el cuerpo es homogéneo de modo que su centro de masas está en algún punto a lo largo del eje principal mayor. Con esto vemos que tanto $\phi$ como $\psi$ son coordenadas cíclicas, con lo que los momentos generalizados asociados se conservan $p_\phi=\frac{\partial L}{\partial \dot \phi}={\cal J}_1(\dot\psi+\dot\phi\,\cos\theta)\cos\theta+{\cal J}_2\sin^2\theta\,\dot\phi=p_\psi\cos\theta+{\cal J}_2\sin^2\theta\,\dot\phi=$ constante $p_\psi=\frac{\partial L}{\partial \dot \psi}={\cal J}_1(\dot\psi+\dot\phi\,\cos\theta)=$ constante Para la coordenada remanente, la ecuación de movimiento será ${\cal J}_2\ddot \theta+{\cal J}_1(\dot\psi+\dot\phi\,\cos\theta)\sin\theta\,\dot\phi-{\cal J}_2\dot\phi^2\,\sin\theta\,\cos\theta-mgl\,\sin\theta=0$ Esta ecuación se simplifica si reemplazamos en ella los valores de $\dot\psi$ y $\dot\phi$ que se obtienen de los momentos generalizados ${\cal J}_2\ddot \theta+p_\psi\sin\theta\left(\frac{p_\phi-p_\psi\cos\theta}{{\cal J}_2\sin^2\theta}\right)-{\cal J}_2\left(\frac{p_\phi-p_\psi\cos\theta}{{\cal J}_2\sin^2\theta}\right)^2\,\sin\theta\,\cos\theta-mgl\,\sin\theta=0$ Lo que deberíamos resolver para obtener el movimiento. Una forma de hacerlo es escribir la energía mecánica $E=K+V$ como $E=\frac12{\cal J}_1(\dot\psi+\dot\phi\,\cos\theta)^2+\frac12{\cal J}_2\left(\dot\theta^2+\sin^2\theta\,\dot \phi^2\right)+mgl\,\cos\theta$ O, reemplazando los valores de los momentos conservados $E=\frac1{2{\cal J_1}}p_\psi^2+\frac1{2{\cal J}_2}\left(\frac{p_\phi-p_\psi\cos\theta}{\sin\theta}\right)^2+\frac12{\cal J}_2\dot\theta^2+mgl\,\cos\theta$ Lo que se puede reescribir como $\underbrace{E-\frac1{2{\cal J_1}}p_\psi^2}_{\cal E}=\frac12{\cal J}_2\dot\theta^2+\underbrace{\frac1{2{\cal J}_2}\left(\frac{p_\phi-p_\psi\cos\theta}{\sin\theta}\right)^2+mgl\,\cos\theta}_{V_{\sf eff}(\theta)}$ Es decir que terminamos escribiendo un sistema unidimensional equivalente con la forma ${\cal E}=\frac12{\cal J}_2\dot\theta^2+V_{\sf eff}(\theta)$ Lo que nos permite despejar $\dot \theta=\sqrt{\frac2{{\cal J}_2}\left({\cal E}-V_{\sf eff}(\theta)\right)}$ Esta ecuación se puede integrar, obteniendo $t=t_0+\int_{\theta_0}^\theta\frac{d\theta}{\sqrt{\frac2{{\cal J}_2}\left({\cal E}-V_{\sf eff}\right)}}$ El potencial diverge para $\theta=0$ y para $\theta=\pi$, por lo que vemos que sea cual fuere la energía ${\cal E}$, siempre tendremos dos puntos de retorno $0<\theta_2 <\theta<\theta_1<\pi$. Es decir que el trompo tendrá un movimiento de *nutación* o cabeceo en el ángulo $\theta$. Nótese que dado que $\dot\phi$ se puede escribir como $\dot \phi=\frac{p_\phi-p_\psi\,\cos\theta}{{\cal J}_2\sin^2\theta}$ Tendremos que en ambos extremos de la oscilación en $\theta$ $\dot \phi_2=\frac{p_\phi-p_\psi\,\cos\theta_2}{{\cal J}_2\sin^2\theta_2}$ $\dot \phi_1=\frac{p_\phi-p_\psi\,\cos\theta_1}{{\cal J}_2\sin^2\theta_1}$ Estas dos velocidades tendrán el mismo signo si $p_\phi/p_\psi>\cos\theta_2$ o si $p_\phi/p_\psi<\cos\theta_1$ (precesión quasiperiódica) y tendrán signos diferentes si $\cos\theta_1<p_\phi/p_\psi<\cos\theta_2$ (precesión alternada). El caso límite es cuando $p_\phi/p_\psi=\cos\theta_2$.  >Ejemplo: supongamos que "soltamos" el trompo en un ángulo fijo, de modo que su velocidad angular inicial es solamente $\vec\omega=\dot\psi_0\check k''$. Entonces tendremos > >$p_\phi={\cal J}_1 \dot\psi_0 \,\cos\theta_0$ > >$p_\psi={\cal J}_1\dot\psi_0$ > >De donde $p_\phi/p_\psi= \cos\theta_0$. Además $\dot\theta_0=0$ por lo que estamos en uno de los puntos de retorno (naturalmente será $\theta_0=\theta_1$). Esto implica que estamos en el caso límite antes mencionado. >Ejercicio: obtenga la velocidad angular de la precesión y la frecuencia y amplitud de la nutación en el caso de un trompo que gira muy rápidamente $\dot\psi\gg {\rm max}(\dot\phi,\dot\theta)$. >Ejercicio: la precesión regular (ausencia de nutación) sucede cuando $\theta_1=\theta_2\equiv\theta_0$. Obtenga la velocidad angular de precesión en ese caso. > Ejercicio: en el trompo vertical $\theta_0=0$, muestre que hay una velocidad crítica más allá de la cual el trompo no nuta. ## Clase 11 ### Vínculos Al principio de la cursada, construimos las ecuaciones de Lagrange escribiendo las leyes de Newton para un sistema de $N$ partículas interactuantes $\vec x_a$ en coordenadas generalizadas $q_i(\vec x_a,t)$, y obteniendo el lagrangiano como $L=K(\dot q_i,q_i,t)-V(q_i)$ donde $K(\dot q_i,q_i)$ es la energía cinética y $V(q_i)$ es la energía potencial, escritas en términos de las coordenadas y velocidades generalizadas. Vimos que esta construcción de podía generalizar a fuerzas monogénicas derivadas de un potencial $V(q_i,t)$ y a fuerzas dependientes de la velocidad (como la fuerza de Lorentz) derivadas de un $U(\dot q_i, q_i, t)$. En nuestros cálculos originales, teníamos $N$ vectores $\vec x_a$, por lo que el sistema tenía $3N$ grados de libertad, cada uno de los cuales tomaba valores en la recta real. Es decir que su espacio de configuración era $\mathbb{R}^{3N}$. Al escribir el sistema en coordenadas generalizadas, siempre estábamos describiendo $\mathbb{R}^{3N}$ y no otra variedad, en coordenadas generales. Sin embargo cuando estudiamos el cuerpo rígido, escribimos un sistema de partículas en términos de coordenadas generalizadas $\vec r_1,\check u,\theta,d_{12},d_{23},d_{31}, d_{a1},d_{a2},d_{a3}$ y luego fijamos el valor de las distancias, en lo que constituye la definición de un cuerpo rígido. El sistema de coordenadas resultante es entonces $\vec r_1,\check u,\theta$ donde $\vec r_1\in\mathbb{R}^3$, $\check u\in S_2$ (aquí $S_2$ es una notación para referirse a la esfera de radio $|\check u|=1$), y $\theta\in S_1$ (aquí $S_1$ denota al círculo unitario). Es decir que el sistema se mueve en $\mathbb{R}^3\times S_2\times S_1$, que es una variedad no trivial. Ahora bien ¿Tiene sentido esta reducción? ¿Cómo sabemos que al dejar fijas las distancias $d_{ij}$ se cumplen las ecuaciones de movimiento correspondientes, siquiera de forma aproximada? A continuación vamos a estudiar las condiciones bajo las cuales tales *vínculos* tienen sentido físico. #### Origen de los vínculos Comencemos con un ejemplo sencillo: sea un sistema de una partícula en una dimensión, con lagrangiano $L=\frac 12 m\dot x^2-V(x)$ La energía de este sistema vendrá dada por $E=\frac 12m\dot x^2+V(x)$ En cualquier situación real, el sistema tiene una energía máxima finita $E_{\sf max}$, es decir que está confinado a moverse en la región del espacio $x\in \mathbb{R}$ donde se satisface $V(x)<E<E_{\sf max}$ Supongamos que el potencial crece con $x$ (si decrece, simplemente podemos cambiar $x$ por $-x$) entonces en un punto $x_+$ se cumple que $V(x_+)=E_{\sf max}$ Por lo que es correcto decir que la evolución temporal del sistema cumplirá $x\leq x_+$ Esta condición se conoce como un *vínculo unilateral*. 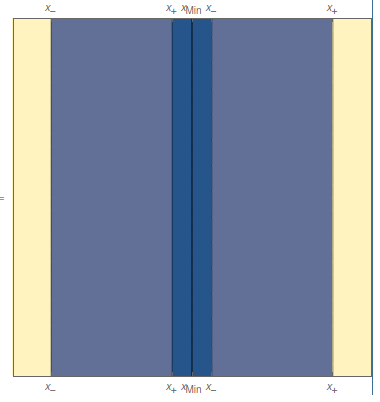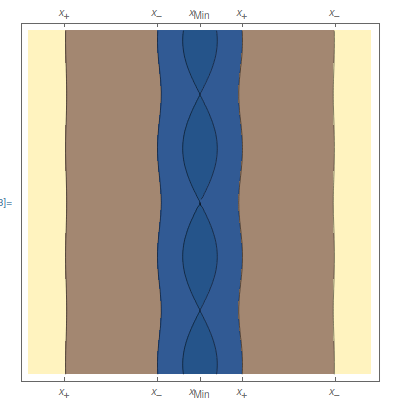Si se cumple que a la izquierda de $x_+$ el potencial tiene un mínimo en $x=x_{\sf min}$, al alejarse hacia la izquierda en la dirección $x<x_{\sf min}$ el potencial también crece, por lo que existirá un segundo punto $x_-$ tal que $V(x_-)=E_{\sf max}$ Lo que por su parte implica un segundo vínculo unilateral $x\geq x_-$ Por lo que el sistema se moverá alrededor de $x_{\sf min}$ entre dos extremos $x_-<x<x_+$. Si el potencial crece muy rápidamente cuando $x$ se aleja de $x_{\sf min}$ en ambas direcciones, esto que implica que la energía alcanzará el valor $E_{\sf max}$ muy rápido tanto a la derecha de $x_{\sf min}$ como a su izquierda. En otras palabras, tendremos que $x_+\approx x_-$, por lo que podemos decir que el sistema está *confinado* al punto $x= x_{\sf min}$ Esto es lo que se conoce como un *vínculo bilateral*.  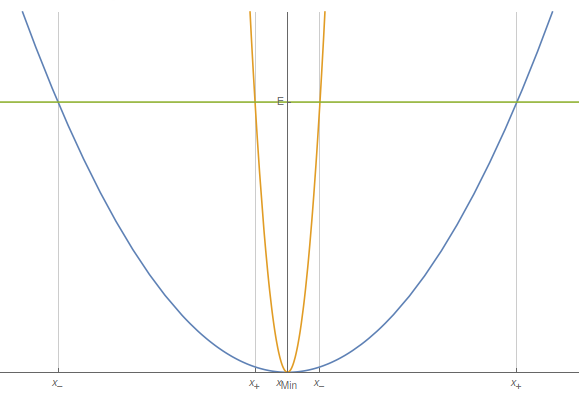Si el potencial es diferenciable en el mínimo, hay una manera alternativa de entender esto. Podemos escribir $V(x)\approx V(x_{\sf min})+\frac12 V''(x_{\sf min})(x-x_{\sf min})^2+{\cal O}(x-x_{\sf min})^3$ Por lo tanto, cerca del mínimo el sistema se comporta como un oscilador armónico con constante restauradora $k=V''(x_{\sf min})$, cuya solución es $x=x_{\sf min}+A\cos\left(\sqrt{\frac {V''(x_{\sf min})}m}t+\varphi\right)$ donde $A$ es la amplitud de la oscilación, y $\varphi$ la fase inicial. La energía de este sistema viene dada por $E = \frac 12 V''(x_{\sf min})\, A^2$ Si tenemos una cierta cantidad máxima de energía $E_{\sf max}$ para poner en el sistema, podemos obtener a partir de ella la amplitud máxima de oscilación, invirtiendo la expresión anterior $A_{\sf max}=\sqrt{\frac {2E_{\sf max}}{V''(x_{\sf min})}}$ Cualquier sistema real tiene una cantidad de energía finita. Por lo tanto, la amplitud de su movimiento será más pequeña cuanto mayor sea la constante restauradora $V''(x_{\sf min})$. Para una constante $V''(x_{\sf min})$ lo bastante grande, es una buena aproximacioń afirmar que el sistema no oscila y está fijo en su punto de equilibrio $x=x_{\sf min}$. Un razonamiento completamente análogo funciona cuando el sistema es bidimensional, pero el pontencial depende de una sola de las coordenadas. $L=\frac 12 m\left(\dot x^2+\dot y^2\right)-V(x)$ La energía de este sistema vendrá dada por $E=\frac 12m\left(\dot x^2+\dot y^2\right)+V(x)$ En cualquier situación real, el sistema tiene una energía máxima finita $E_{\sf max}$, es decir que está confinado a moverse en la región del espacio $x\in \mathbb{R}$ donde se satisface $V(x)<E<E_{\sf max}$ Supongamos un potencial creciente en ambas direcciones $x\to \pm\infty$, esto implica la existencia de los vínculos unilaterales $x_-<x<x_+$ A medida que el potencial se haga más empinado, creciendo más rapidamente a medida que nos alejamos hacia la izquierda o la derecha del mínimo, el sistema está cada vez más confinadoa moverse cerca del mínimo, por lo que en el límite obtenemos el vínculo bilateral, igual que antes $x=x_{\sf min}$  En otras palabras, el sistema reduce su dimensión, estando ahora confinado a moverse solamente en $y$, con el lagrangiano $L_{\sf efectivo}=\frac 12 m \dot y^2$ Lo interesante es que esta situación también sucede cuando el potencial depende de las dos variables, pero mucho más fuertemente de una (digamos $x$) que de la otra $L=\frac 12 m\left(\dot x^2+\dot y^2\right)-V(x,y)$ En efecto, en ese caso la condición $V(x,y)<E<E_{\sf max}$ Resulta en los vínculos unilaterales $x_-(y)<x<x_+(y)$ De nuevo, estos vínculos se irán acercando a medida que el potencial se hace más empinado en la dirección $x$, resultando finalmente en el confinamiento del sistema a moverse en una dimensión, a lo largo del vínculo bilateral $x=x_{\sf min}$ con el lagrangiano $L_{\sf efectivo}=\frac 12 m\dot y^2-V(x_{\sf min},y)$  Por supuesto, este fenómeno no tiene por qué restringirse a coordenadas cartesianas. Supongamos que tenemos un sistema escrito en coordenadas polares, tal que el potencial depende solo del radio $L=\frac 12 m\left(\dot r^2+r^2\dot \theta^2\right)-V(r)$ Si el potencial tiene un mínimo en $r=r_{\sf min}$, el hecho de que siempre habrá una cantidad finita de energía $E<E_{\sf max}$ hace que el sistema se mueva en una región acotada por dos vínculos unilaterales $r_-<r<r_+$. cuando el potencial sea muy empinado, el sistema se moverá cumpliendo el vínculo bilateral $r=r_{\sf min}$  El lagrangiano efectivo será entonces $L_{\sf efectivo}=\frac 12 m r^2_{\sf min}\dot \theta^2$ Nuevamente, no es necesario que no haya dependencia explícita del potencial en la variable adicional, en este caso $\theta$, alcanza con que sea una dependencia mucho más suave que en la variable vinculada, en este caso $r$. En ese caso obtendríamos un lagrangiano efectivo $L_{\sf efectivo}=\frac 12 m r^2_{\sf min}\dot \theta^2-V(r_{\sf min},\theta)$  En general, podemos escribir un lagrangiano para un sistema con $N$ partículas en términos de $3N$ coordenadas generalizadas, según $L(\dot q_i,q_i)$ con $i\in\{1,\dots,3N\}$ Para un conjunto de partículas no relativistas sometidas a una fuerza conservativa, este lagrangiano tomará necesariamente la forma $L=\frac 12 K_{ij}(q_i)\dot q_i\dot q_j-V(q_i)$ La energía del sistema siempre estará acotada, y por lo tanto se cumple que $V(q_i)<E<E_{\sf max}$ Al igual que en el caso bidimensional, esto establece vínculos unilaterales en las coordenadas. Cuando el potencial depende muy fuertemente de alguna de las coordenadas, creciendo hacia ambos lados de un valor mínimo aparece un vínculo unilateral a cada. Si el potencial crece muy rápidamente al alejarse del valor mínimo, estos pares de vínculos unilaterales se juntan y se transforman en bilaterales. Suponiendo que elegimos las coordenadas de tal modo que a lo largo de las coordenadas $q_k$ con $k\in\{1,\dots,p\}$ el potencial presenta mínimos al moverse en cada una de estas coordenadas dejando las demás fijas, mientras que a lo largo de $q_l$ con $l\in\{p+1,\dots,3N\}$ la dependencia del potencial es mucho más suave, en ese caso hay pares de vínculos unilaterales que se juntan en valores fíjos de cada una de las $q_k$ digamos $q_k=0$. En terminos de las coordendas cartesianas de las partículas $\vec x^a\in \mathbb{R}^{3N}$, el sistema se mueve en una hipersuperficie de dimensión $3N-p$ determinada por las condiciones $q_k(\vec x^a)=0$ con $k\in\{1,\dots,p\}$ Por lo tanto, podemos describir el movimiento con el lagrangiano efectivo $L_{\sf efectivo}=\frac 12 K_{lm}(q_l, q_k\!=\!0)\dot q_l\dot q_m-V(q_l,q_k\!=\!0)$ #### Multiplicadores de Lagrange Es interesante destacar que si bien es posible resolver los vínculos en términos de un nuevo conjunto de coordenadas generalizadas, no siemrpe es útil hacerlo. Podemos también usar la técnica de los *multiplicadores de Lagrange* para incorporar los vínculos en el Lagrangiano > Ejemplo: supongamos que tenemos una partícula en el plano con un vínculo dado por > > $x^2+y^2=R^2$ > > Es decir que la partícula está confinada a moverse en un anillo. > >Supongamos que obedece a una dinámica de partícula libre, es decir que el lagrangiano será > > $L=\frac12m\left(\dot x^2+\dot y^2\right)$ > > Podemos pasar a un sistema de coordenadas polares, para obtener > > $L=\frac 12 m \left(\dot r^2+r^2\dot \theta^2\right)$ > > con el vínculo > > $r=R$ > > Las ecuaciones de movimiento serán > > $m\ddot r- m r\dot\theta^2=0$ > $\frac d{dt}\left(mr^2\dot \theta\right)=0$ > > si reemplazamos el vínculo en las ecuaciones de movimiento tenemos > > $m R\dot\theta^2=0$ > $\frac d{dt}\left(mR^2\dot\theta\right)=0$ > > con lo que la solución será necesariamente $\dot\theta=0$. > > Sin embargo, si hubiéramos reemplazado primero el vínculo en el lagrangiano, obteniendo > > $L=\frac 12mR^2\dot\theta^2$ > > sólo hubiéramos obtenido la ecuación > > $\frac d{dt}\left(mR^2\dot\theta\right)=0$ > > > la cual permite soluciones más generales $\dot\theta=\omega$ constante. Es evidente que un sistma formado por una partícula confinada a moverse en un círuclo tendrá solucioens de este tipo, por lo que algo hicimos mal más arriba al reemplazar el vínculo antes de resolver las ecuaciones. La respuesta es evidente: el movimiento radial está sometido a fuerzas que son las responsables de que la partícula quede confinada al círculo, en las ecuaciones que obtivimos más arriba esas *fuerzas de vínculo* están ausentes. El conjunto correcto d ecuaciones debería verse algo así > > $m\ddot r- m r\dot\theta^2=F_{\sf vinc}$ > $\frac d{dt}\left(mr^2\dot \theta\right)=0$ > > ¿Como hacemos para obtener $F_{\sf vinc}$? Una opción es insertar la solución de la segunda ecuación en la primera, de donde se obtiene $F_{\sf vinc}=-mR\omega^2$. Otra opción es agregar un potencial $V_{\sf vinc}$ al lagrangiano, obteniendo > > $L'=L-V_{\sf vinc}$ > > lo que implica > > $m\ddot r- m r\dot\theta^2=-V'_{\sf vinc}$ > $\frac d{dt}\left(mr^2\dot \theta\right)=0$ > > Una forma posible para el potencial, que nos daría la forma correcta de la fuerza de vínculo es $V_{\sf vinc}=-\lambda(r-R)$ con $\lambda$ una constante ajustable para que se cumplan las ecuaciones, que terminará siendo igual a $-m\omega^2R$. > > Ahora bien, no podemos saber el valor de $\omega$ hasta no resolver las ecuaciones de movimiento, por lo que no sería correcto incluir $\omega$ en el lagrangiano, que es algo que se tiene antes de las ecuaciones. Por esta razón, es preferible promover $\lambda$ a una coordenada más, en un pie de igualdad con $r$ y $\theta$, con lo que tenemos > > $L'=L+\lambda (r-R)$ > > Lo que resulta en las ecuaciones de movimiento > > $m\ddot r- m r\dot\theta^2=\lambda$ > $\frac d{dt}\left(mr^2\dot \theta\right)=0$ > $r-R=0$ > > La última líena es la ecuación de Lagrange para la nueva variable $\lambda$, la cual reobtiene el vínculo, ahora como una ecuación de movimiento. El procedimiento del ejemplo anterior se puede generalizar. Supongamos que tenemos un lagrangiano $L$ con $3N$ coordenadas generalizadas $q_i$, y $p$ vínculos dados por $f_k(q_i)=0$ con $k\in\{1,\dots,p\}$ En lugar de resolver los vínculos en términos de un nuevo conjunto de coordenadas genralizadas y reemplazar la solución en el lagrangiano, podemos modificar el lagrangiano agregando las fuerzas de vínculo, de la forma $L'=L+\lambda_k f_k(q_i)$ Las nuevas coordenadas $\lambda_k$ son funciones del tiempo que se llaman *multiplicadores de Lagrange* y se tratan en un pie de igualdad con las $q_i$. El tipo de vínculos que venimos discutiendo se denominan *holonómicos*, porque están dados como un conjunto de relaciones entre las coordenadas de la forma $f_k(q_i)=0$ con $k\in\{1,\dots,p\}$ Estas relaciones pueden resolverse en términos de un nuevo conjunto de coordenadas generalizadas, de modo que las relaciones se traducen en dejar fijas $p$ de las $3N$ coordeandas. De las $3N$ coordenadas originales quedan $3N-p$ *grados de libertad*. El tipo de vínculos holonómicos que venimos discutiendo se llaman vínculos *reonomos* porque no dependen del tiempo. En el caso de que el potencial dependa del tiempo, no hay una energía conservada. Sin embargo, si el potencial cambia lo bastante lentamente comparado con las velocidades características del movimiento, podemos reproducir los razonamientos anteriores para escribir vínculos *esclerónomos* de la forma $f_k(q_i, t)=0$ con $k\in\{1,\dots,p\}$ Nuevamente, estos vínculos pueden resolverse en términos de un nuevo conjunto de coordenadas generalizadas, de modo que se tradzcan en dejar fijas $p$ de las $3N$ coordeandas. Y otra vez de las $3N$ coordenadas originales quedan $3N-p$ *grados de libertad*. Existen también situaciones más generales que las que hemos discutido, el las cuales el sistema queda sometido a vínculos no-holonómicos, en donde la restriccion involucra a las velocidades $f_k(q_i,\dot q_i)=0$ con $k\in\{1,\dots,p\}$ > Ejemplo: si tenemos una rueda de radio $R$ en que se mueve en una dimensión el, estado de la rueda está caracterizado por su posición $x$ y el ángulo que lleva rotado respecto de su posición inicial $\phi$. Estas variables satisfacen el vínculo *de rodadura* > > $dx=R\,d\phi$ > >Lo que se puede reescribir como > >$\dot x-R\dot \phi=0$ > > Este es un vínculo no-holonómico. En el caso de una dimensión el vínculo se puede integrar para obtener > > $x-x_0-R(\phi-\phi_0)=0$ > > Es decir que lo hemos transformado en un vículo holonómico, par ael cual podemos definir las nuevas coordenadas > > > $q_1=x-x_0-R(\phi-\phi_0)$ > $q_2=q_2(x,\phi)$ > > Con lo que vemos que el sistema tiene un solo grado de libertad dado por $q_2$ > Ejemplo: si tenemos una rueda de radio $R$ que ahora se mueve en dos dimensiones, entonces > >$d\ell=R\,d\phi$ > > Lo que se puede reescribir como > > $\sqrt{dx^2+dy^2}=R\,d\phi$ > > O bien > > $\sqrt{\dot x^2+\dot y^2}-R\dot \phi=0$ Los vínculos no holonómicos no se pueden resolver en términos de un nuevo conjunto de coordenadas generalizadas. Sin embargo, siempre se pueden tratar usando el método de los multiplicadores de Lagrange. En el caso general en el cual tenemos un lagrangiano $L(\dot q_i,q_i,t)$ ## Clase 12 ### Pequeñas oscilaciones  #### Caso sencillo unidimensional Supongamos que tenemos un sistema unidimensional no relativista. Su lagrangiano tendrá necesariamente la forma $L=\frac 12m \dot x^2-V(x)$ Las ecuaciones de movimiento resultantes serán, por supuesto $m\ddot x=-V'(x)$ Puede resultar más o menos complejo resolver esta ecuación para un potencial cualquiera $V(x)$. Sin embargo, si el potencial tiene un punto estacionario en $x_0$, es decir que $V'(x_0)=0$ una solución trivial de estas ecuaciones es la constante $x=x_0$. Nos preguntamos entonces qué pasa si expandimos en potencias del desplaramiento respecto a $x_0$, en otras palabras si escribimos $x=x_0+\delta x$ con $\delta x$ lo suficientemente pequeño. En ese caso, el Lagrangiano se escribe $L=\frac 12m\left(\dot x_0+\dot {\delta x}\right)^2-V(x+\delta x)$ Expandiendo en potencias de $\delta x$ tenemos $L\approx \frac 12m\,\dot{\delta x}^2-V(x_0)-V'(x_0)\,\delta x-\frac12 V''(x_0)\delta x^2+{\cal O }(\delta x)^3$ El término $V(x_0)$ es una constante que no afectará las ecuaciones de movimiento (ya que las mismas se obtienen de tomar derivadas respecto de $\delta x$, y la constante no contiene $\delta x$). Por otro lado, el término lineal $V'(x_0)\delta x$ se anula porque $x_0$ es un punto estacionario del potencial. Nos queda $L\approx \frac 12m\,\dot{\delta x}^2-\frac12 k\,\delta x^2+{\cal O}(\delta x)^3$ Donde $k=V''(x_0)$. Este es el lagrangiano ed un oscilaor armónico, como puede verse obteniendo sus ecuaciones de movimiento $m\,\ddot {\delta x}+k\,\delta x+{\cal O}(\delta x)^2=0$ Si escribimos el Ansatz $\delta x= c \,e^{i\omega \,t}$ y descartamos los órdenes cuadráticos, nos queda $(m-\omega^2k)c=0$ Esto se satisface siempre que $\omega=\pm\sqrt{k/m}$, para cualquier valor de $c$, lo que nos permite elegir convencionalmente $c=1/\sqrt m$. Entonces la solución general será $\delta x= {\Re}\left(A^+e^{i\omega\,t}+A^-e^{-i\omega \,t}\right)$ con $A^\pm$ constantes arbitrarias. Nótese que $\omega$ viene dado por la raiz cuadrada de $k/m=V''(x_0)/m$. Por lo tanto, si el punto estacionario $x_0$ del potencial es un mínimo, $\omega$ será real y las exponenciales en la expresión anterior serán sumas de senos y cosenos. Tomando la parte real obtenemos $\delta x = A \cos(\omega \,t+\varphi)$ Con $A$ y $\varphi$ obtenibles en términos de $A^\pm$ y $m$. > Ejercicio: encontrar la forma explícita de $A$ y $\varphi$ en términos de $A^\pm$ Si en cambio $x_0$ es un máximo del potencial, entonces $\omega$ será imaginario, y la solución quedará escrita como $\delta x= {\Re}\left(A^+e^{-|\omega|\,t}+A^-e^{|\omega| \,t}\right)$ Aquí vemos que uno de los términos tiende a cero exponencialmente, mientras que el otro diverge. Esto quiere decir que cualquier perturbación $\delta x$ alrededor del máximo $x_0$ saca al sistema del punto estacionario y lo hace caer por el potencial. Por supuesto cuando esto sucede, la solución que obtuvimos sólo es válidad por un pequeño intervalo de tiempo, ya que para obtenerla asumimos que $\delta x$ era pequeño. La idea es generalizar esto para más variables y para sistemas más complicados. > Nota acerca de soluciones complejas: en lo anterior la solución del problema se obtuvo tomando la parte real $\Re(\cdot)$ de una expresión compleja. > > Esto se justifica como sigue. Tomemos nuestra ecuación inicial > > $m\ddot {\delta x}+k\,\delta x=0$ > > Inventemos una magnitud diferente $\bar{\delta x}$ que satisface la misma ecuación de movimiento, es decir > > $m\ddot {\bar{\delta x}}+k\,\bar{\delta x}=0$ > > y ahora escribamos la magnitud compleja $\hat{\delta x}=\delta x+i\,\bar{\delta x}$. Sumando las ecuacions diferenciales, la segunda multiplicada por $i$, vemos que esta magnitud compleja satisface > > $m\ddot {\hat{\delta x}}+k\,\hat{\delta x}=0$ > >Es decir que $\hat{\delta x}$ satisface una ecuación de movimiento idéntica a la de ${\delta x}$. Es entonces para la magnitud $\hat{\delta x}$ que se propone la forma $\hat{\delta x}=c\,e^{i \omega \,t}$ y se resuelven las ecuaciones. Y luego al final del cálculo se toma la parte real para recuperar $\delta x=\Re(\hat {\delta x})$. Nótese que en este proceso las constantes $A^\pm$ podrían en principio haberse elegido complejas. > > Nótese que para poder escribir para $\hat{\delta x}$ una ecuación de movimiento que terminó teniendo exactamente la misma forma que la de $\delta x$, fue crucial que la ecuación para $\delta x$ fuera lineal. Si hubiera habido por ejemplo un $\delta x^2$ en algún lado, o alguna función más compliicada de $\delta x$, nos hubiera resultado imposible. > > Sin embargo, es evidente que no se gana mucho con hacer estas consideraciones cada vez que se resuelve una ecuación lineal, por eso y salvo que haya dudas, en adelante omitiremos hacerlas y nos refeririremos indistintamente a $\hat {\delta x}$ y a su parte real $\Re(\hat {\delta x})$ como $\delta x$. #### Caso unidimensional más general Empecemos con un sistema unidimensional general que depende de una coordenada $q$. Su lagrangiano se escribirá $L=L(\dot q, q, t)$ y sus ecuaciones de movimiento serán $\frac d{dt}\left(\frac{\partial L}{\partial \dot q}(\dot q,q,t)\right)-\frac{\partial L}{\partial q}(\dot q, q, t)=0$ Vamos a suponer que existe una solución estática $q=q_0$, $\dot q=0$. Como veremos, no cualquier Lagrangiano unidimensional las tiene. En efecto, si reemplazamos esta solución en las ecuaciones de movimiento, obtenemos $\frac d{dt}\left(\frac{\partial L}{\partial \dot q}(0,q_0,t)\right)-\frac{\partial L}{\partial q}(0, q_0, t)=0$ Es decir que se tiene que cumplir que $\frac{\partial^2 L}{\partial t\,\partial \dot q}(0,q_0,t)=\frac{\partial L}{\partial q}(0, q_0, t)$ Esta condición es el equivalente para este problema un poco más general, de la condición de punto estacionario del caso analizado más arriba. Para ver esto, notemos que si el lagrangiano no depende del tiempo, esto se simplifica $\frac{\partial L}{\partial q}(0, q_0)=0$ Y si el lagrangiano tiene la forma de más arriba, recuperamos la condición de punto estacionario. Ahora bien, si queremos expandir alrededor de esta solución estatica, escribimos $q=q_0+\delta q$ y reemplazamos en $L$ para obtener $L=L_0 +\frac{\partial L}{\partial \dot q}\,\dot {\delta q}+\frac{\partial L}{\partial q} \,{\delta q}+\frac 12\left(\frac{\partial^2L}{\partial \dot q^2}\dot{\delta q}^2+ \frac{\partial^2L}{\partial q^2}{\delta q}^2+2\frac{\partial^2L}{\partial\dot q\partial q}\delta q\dot{\delta q}\right)$ donde $L$ y sus derivadas están evaluados en $(0,q_0,t)$. El primer término no depende de las varaibles respecto de las cuales vamos a derivar para obtener las ecuaciones de movimiento, por lo que no influirá en ellas y puede ser omitido. Los términos lineales tampoco influirán en las ecuaciones de movimiento porque se cumple la condición análoga a la de punto estacionario escrita más arriba. En efecto, si escribimos las ecuaciones, tenemos $\frac{\partial^2 L}{\partial t\,\partial \dot q}+\frac d{dt}\left(\frac{\partial^2L}{\partial\dot q^2}\,\dot{\delta q} + \frac{\partial^2L}{\partial\dot q\partial q}\delta q\right)-\frac{\partial L}{\partial q}-\frac{\partial^2L}{\partial q^2}{\delta q}-\frac{\partial^2L}{\partial\dot q\partial q}\dot{\delta q}=0$ El primero y el tercer término se cancelan, en virtud de la condición que escribimos más arriba, análoga a la de punto estacionario, como anticipamos. Nos queda $\frac d{dt}\left(\frac{\partial^2L}{\partial\dot q^2}\,\dot{\delta q} + \frac{\partial^2L}{\partial\dot q\partial q}\delta q\right)-\frac{\partial^2L}{\partial q^2}{\delta q}-\frac{\partial^2L}{\partial\dot q\partial q}\dot{\delta q}=0$ Al aplicar la derivada temporal a cada término dentro del paréntesis, el término lineal en $\dot{\delta q}$ tambien se cancela, quedando $\frac d{dt}\big{(}\underbrace{\frac{\partial^2L}{\partial\dot q^2}}_{m(t)}\,\dot{\delta q}\big{)} +\underbrace{\left(\frac \partial{\partial t}\left( \frac{\partial^2L}{\partial\dot q\partial q}\right)-\frac{\partial^2L}{\partial q^2}\right)}_{k(t)}{\delta q}=0$ o en otras palabras, terminamos con un *problema de Sturm-Liuville* de la forma $\frac{d}{dt}\left(m(t)\frac{d\delta q}{dt}\right)+k(t)\,\delta q=0$ Estos problemas se estudian en Matemáticas Especiales II. Aquí solo diremos que en general esa ecuación lineal de segundo orden tiene dos soluciones linealmente independientes $f^{\pm}(t)$, y que cualquier otra solucíón será una combinación lineal de ellas $\delta q(t)=A^+f^+(t)+A^-f^-(t)$ Nótese que aquí $\pm$ es solo una notación para distinguir dos soluciones, y no se refiere al signo de ninguna frecuencia, ya que $f^\pm(t)$ no son en general soluciones oscilatorias ni exponenciales. > En este punto podemos apliar el alcance de lo discutido observando que, si en lugar de una solución estática hubieramos desarrollado alrededor de una solución dinámica $q(t)$, hubiéramos terminado con una ecuación similar. En el caso de que el lagrangiano no dependa del tiempo, ni $m$ ni $k$ dependen del tiempo, por lo que la ecuación vuelve a tomar la forma de un oscilador armónico $m\,\ddot{\delta q}+k\,\delta q=0$ donde ahora $m$ y $k$ se obtienen del lagrangiano según $m=\frac{\partial^2L}{\partial\dot q^2}(0,q_0)$ $k=\frac{\partial^2L}{\partial q^2}(0,q_0)$ De nuevo la solución estará dada por la expresión de más arriba $\delta q(t)= \Re\left(A^+e^{i\omega \,t}+A^-e^{-i\omega\,t}\right)$ Y será oscilatoria siempre que $m$ y $k$ sean positivos. Nótese que ahora hay dos posibles fuentes de inestabilidad, que podrían hacer que $\omega$ sea imaginario: podríamos tener $k$ negativo, lo que implicaría un máximo de potencial, o podríamos tener $m$ negativo, que implicaría que la inestabilidad proviene de la energía cinética. La primera inetabilidad se llama *taquiónica* o *por taquiones* y la segunda se denomina *por fantasmas*. #### Caso bidimensional simple Supongamos el lagrangiano de una partícula sometida a un potencial bidimensional en coordenadas cartesianas $L = \frac 12 m\left(\dot x^2+\dot y^2\right)-V(x,y)$ De nuevo, supongamos que $(x_0,y_0)$ es un punto estacionario del potencial, que cumple $\frac{\partial V}{\partial x}(x_0,y_0)=\frac{\partial V}{\partial y}(x_0,y_0)=0$ Escribiendo una pequeña perturbación alrededor del punto estacionario como $x=x_0+\delta x$, $y=y_0+\delta y$ y desarrollando a segundo orden de las perturbaciones $\delta x,\delta y$, nos queda $L = \frac12m\left(\dot{\delta x}^2+\dot{\delta y}^2\right)-V(x_0,y_0)-\frac{\partial V}{\partial x}\delta x-\frac{\partial V}{\partial y}\delta y+$ $-\frac12\left(\frac{\partial^2V}{\partial x^2}\delta x^2+\frac{\partial^2V}{\partial y^2}\delta y^2+2\frac{\partial^2V}{\partial x\partial y}\delta x\delta y\right)+{\cal O}(\delta^3)$ En la primera línea, el segundo término es una constante qu eno depende de $\delta x$ ni $\delta y$ ni de sus derivadas, y por lo tanto no afectará las ecuaciones de movimiento. En cuanto a los últimos dos términos, se desvancen por la condición de punto estacionario. Eso nos deja con $L = \frac12m\left(\dot{\delta x}^2+\dot{\delta y}^2\right)-\frac12\left(\frac{\partial^2V}{\partial x^2}\delta x^2+\frac{\partial^2V}{\partial y^2}\delta y^2+2\frac{\partial^2V}{\partial x\partial y}\delta x\delta y\right)$ lo que implica las ecuaciones de movimiento $m\ddot{\delta x}+k_{xx}\delta x+k_{xy}\delta y=0$ $m\ddot{\delta y}+k_{yy}\delta y+k_{xy}\delta x=0$ donde hemos definido las magnitudes $k_{xx}=\frac{\partial^2V}{\partial x^2}$ $k_{yy}=\frac{\partial^2V}{\partial y^2}$ $k_{xy}=\frac{\partial^2V}{\partial x\partial y}$ Si escribimos en Ansatz $\delta x=c_xe^{i\omega\,t }$, $\delta y=c_ye^{i\omega\,t}$ nos queda $\left(k_{xx}-m\omega^2\right)c_x+k_{xy}c_y =0$ $\left(k_{yy}-m\omega^2\right)c_y+k_{xy}c_x=0$ > Caso sencillo: si $k_{xy}=0$, las ecuaciones *se desacoplan*, en el sentido de que la ecuación para $c_x$ no contiene $c_y$ y viceversa. Entonces de la primera ecuación podemos despejar la frecuenia obteniendo que $\delta x$ es un oscilador armónico con frecuencia $\omega_x=\pm \sqrt{k_{xx}/m}$, y haciendo lo mismo en la segunda vemos que $\delta y$ es otro con frecuencia $\omega_y=\pm \sqrt{k_{yy}/m}$. Además se ve en las ecuaciones que podemos poner $c_x=c_y=1/\sqrt{m}$. En ese caso la solución se escribe > > $\delta x= \Re\left(A^+_xe^{i\omega_xt}+A^-_xe^{-i\omega_xt}\right)$ > $\delta y= \Re\left(A_y^+e^{i\omega_yt}+A^-_ye^{-i\omega_yt}\right)$ > > Aquí vemos que ambas perturbaciones oscilarán cuando el potencial tenga un mínimo en el punto estacionario, ya que en ese caso tanto $k_{xx}$ como $k_{yy}$ serás positivas. Por otro lado, si el potencial tuviera un máximo en el punto estacionario, ambas perturbaciones serían inestables, creciendo esponencialmente. En el caso de que le punto estacionario sera un punto de ensilladura, entonces una de las dos pertubaciones oscilará mientras que la otra será inestable y crecerá exponencialemnte. En el caso general con $k_{xy}\neq 0$ tenemos que resolver $\left(k_{xx}-m\omega^2\right)c_x+k_{xy}c_y =0$ $\left(k_{yy}-m\omega^2\right)c_y+k_{xy}c_x=0$ Multiplicando la primera ecuación por $\left(k_{yy}-m\omega^2\right)$ y la segunda por $k_{xy}$ y restando, obtenemos $\left(\left(k_{yy}-m\omega^2\right)\left(k_{xx}-m\omega^2\right)-k_{xy}^2\right)c_x=0$ Para que se anule el prefactor tiene que cumplirse que $m^2{\omega^2}^2-m(k_{xx}+k_{yy})\omega^2+k_{xx}k_{yy}-k_{xy}^2=0$ Esto es una ecuación cuadrática para $\omega^2$, o que nos da la solucion $\omega^2_{1,2}=\frac{k_{xx}+k_{yy}}{2m}\pm\sqrt{\left(\frac{k_{xx}+k_{yy}}{2m}\right)^2-\frac{k_{xx}k_{yy}-k_{xy}^2}{m^2}}$ Por lo tanto, hay dos frecuencias posibles para este sistema dependiendo de la elección de signo en esta solución. Esto se puede reescribir como $\omega^2_{1,2}=\frac{1}{2m}\left(k_{xx}+k_{yy}\pm\sqrt{(k_{xx}-k_{yy})^2+4k_{xy}^2}\right)$ Con lo que vemos que ambas soluciones satisfacen $\omega^2_{1,2}\in\mathbb{R}$. Todavía nos falta resolver para $c_x$ y $c_y$. Primero notemos que las ecuaciones determinan esas magnitudes a menos de una constante multiplicativa. En efecto, si tomamos cualquier solución $c_x, c_y$ y multimplicamos ambas magnitudes por el mísmo número, obtenemos otra solución. Esto nos permite elegir $m(c_x^2+c_y^2)=1$ o en otras palabras $c_x=(1/\sqrt m)\cos\alpha$, $c_y=(1/\sqrt m)\sin\alpha$ para algún angulo $\alpha$. Con esto, las ecuaciones nos quedan $\left(k_{xx}-m\omega^2\right)\cos\alpha=-k_{xy}\sin\alpha$ $\left(k_{yy}-m\omega^2\right)\sin\alpha=-k_{xy}\cos\alpha$ Dividiendo estas ecuaciones se obtiene $\tan^2\alpha_{1,2}=\frac{k_{xx}-m\omega^2_{1,2}}{k_{yy}-m\omega^2_{1,2}}$ De donde vemos que hay dos soluciones $\alpha_{1,2}$, correspondientes a las frecuencias $\omega_{1,2}$. Con esto, nuestra solución general para el probelma se podrá escribir como $\delta x=\frac1{\sqrt m}\Re\left(\cos\alpha_1(A_{1}^+e^{i\omega_1t}+A^-_{1}e^{-i\omega_1t})+\cos\alpha_2(A_{2}^+e^{i\omega_2t}+A^-_{2}e^{-i\omega_2t})\right)$ $\delta y=\frac1{\sqrt m}\Re\big{(}\sin\alpha_1\underbrace{(A_{1}^+e^{i\omega_1t}+A^-_{1}e^{-i\omega_1t})}_{\delta u}+\sin\alpha_2\underbrace{(A_{2}^+e^{i\omega_2t}+A^-_{2}e^{-i\omega_2t})}_{\delta v}\big{)}$ donde $A_{1,2}^\pm$ son constantes arbitrarias. Nótese que ahora la estabilidad o inestabilidad del sistema estará determinada por los valores reales o imaginarios de ambas frecuencias $\omega_{1,2}$. ¿Qué representan estas dos soluciones? Para entender esto, reescribamos lo anterior como $\delta x=\frac1{\sqrt m}\left(\cos\alpha_1\,\delta u+\cos\alpha_2\,\delta v\right)$ $\delta y=\frac1{\sqrt m}\left(\sin\alpha_1\,\delta u+\sin\alpha_2\,\delta v\right)$ Reemplazando en el lagrangiano nos queda $L=\frac 12\left(\dot{\delta u}^2+\dot{\delta v}^2\right)+\frac1{2}\left(\omega_1^2\,\delta u^2+\omega_2^2\,\delta v^2\right)$ >Ejercicio: pruebe este último resultado, recuerde utilizar la relación entre $\omega_{1,2}$ y $\tan \alpha_{1,2}$ En este cálculo $\delta u$ y $\delta v$ son los *modos normales* del sistema, y corresponden a rotar las direcciones $\delta x$ y $\delta y$ hacia las direcciones de máximo y mínimo cambio del potencial. Todo el cálculo de esta sección se puede simplificar si lo escribimos en términos de matrices. Para eso, ponemos $\vec{\delta x}=(\delta x,\delta y)$ $k=\left(\begin{array}{cc}k_{xx}&k_{xy}\\k_{xy}&k_{yy}\end{array}\right)=H(V)$ con lo que el lagrangiano nos queda $L=\frac12 m\,\vec{\delta x}^2-\frac12\,\vec{\delta x}^t\cdot k\cdot\vec{\delta x}$ y las ecuaciones de movimiento se leen $m\ddot{\vec{\delta x}}+k\cdot\vec{\delta x}=0$ usando el Ansatz $\vec{\delta x}=\vec c\,e^{i\omega\,t}$ tenemos $\left(k-m\omega^2\,I\right)\cdot\vec{c}=0$ Esto es una ecuación de autovalores donde $m\omega^2$ sería un autovalor de la matriz $k$. Nótese que esta ecuación determina $\vec c$ a menos de una constante multiplicativa, por lo que podemos elegir $m\vec c^2=1$ de donde $\vec c=(1/\sqrt m)(\sin\alpha,\cos\alpha)$ para algún ángulo $\alpha$. Para que esta ecuación tenga una solución no trivial, se tiene que cumplir que ${\sf Det}\left(k-m\omega^2\,I\right)=0$ Esto no es más que la ecuación cuadŕatica en $\omega^2$ que obtuvimos más arriba de donde despejamos las dos soluciones $\omega_{1,2}$. Esto implica que habrá en principio dos soluciones diferentes para $\vec c$ que podemos llamar $\vec c_{1,2}$. Estas cumplen que $k\cdot\vec c_1=m\omega_1^2\vec c_1$ $k\cdot\vec c_2=m\omega_2^2\vec c_2$ Multiplicando cada ecuación por el vector $\vec c_{1,2}$ correspondiente, obtenemos $\vec c_{1,2}^t\cdot k\cdot \vec c_{1,2}=\omega_{1,2}^2$ de donde vemos que el signo de $\omega^2_{1,2}$, y consecuentemente la estabilidad del sistema, dependerán del signo de $\vec c_{1,2}^t\cdot k\cdot \vec c_{1,2}$, que es la variación en el potencial cuando nos movemos del punto estacionario una distancia $\vec c_{1,2}$. Si esta cantidad es positiva, es decir si estamos en un mínimo de potencial, entonces ambas frecuencias son relaes. Si en cmabio es negativa, es decir si estamos en un máximo del potencial, ambas serán imaginarias y aparecerá una inestabilidad. Puede darse también que estemos en un punto silla, y que la magnitud sea positiva para $\vec c_1$ y negativa para $\vec c_2$, implicando que habrá estabilidad ne una dirección e inestabilidad en otra. Si ahora multiplicamos la primera ecuación por $\vec c_2^t$ y la segunda por $\vec c_1^t$ y las restamos tenemos que $m(\omega_1^2-\omega_2^2)\,\vec c_2^t\cdot\vec c_1=0$ Esto implica que si $\omega_1\neq\omega_2$ entonces $\vec c_1\perp\vec c_2$. La solución general puede entonces escribirse $\vec {\delta x}=\Re\big{(}\underbrace{\left(A^+_1e^{i\omega_1 t}+A^-_1e^{-i\omega_1 t}\right)}_{\delta u}\vec c_1+\underbrace{\left(A^+_2e^{i\omega_2 t}+A^-_2e^{-i\omega_2 t}\right)}_{\delta v}\vec c_2\big{)}$ con lo que los modos normales nos quedan escritos según $\vec{\delta x}=\delta u\,\vec c_1+\delta v\,\vec c_2$ En el Lagrangiano esto implica que $L=\frac12\left(\dot{\delta u}^2+\dot{\delta v}^2\right)-\frac 12 \left(\omega_1^2\delta u^2+\omega_2^2\delta v^2\right)$ $=\frac12\left(\dot{\delta u}^2-\omega^2_1{\delta u}^2\right)+\frac12\left(\dot{\delta v}^2-\omega^2_2{\delta v}^2\right)=L_1+L_2$ Donde $L_{1,2}$ representan dos osciladores armónicos independientes, cada uno con una de las frecuencias $\omega_{1,2}$. ## Clase 13 #### Caso multidimensional un poco más complicado Ahora vamos a generalizar lo anterior en dos direcciones: vamos a agregar un número arbitrario de coordenadas, y vamos a permitir un lagrangiano ligeramente más general, con la forma $L(\dot q_i,q_i) = K(\dot q_i, q_i) - V(q_i)$ Este aún no es el lagrangiano más general posible, ya que restringiremos la energía cinética a ser una forma cuadrática en las velocidades. $K(\dot q_i, q_i)=\frac 12 K_{ij}(q_k)\,\dot q_i\dot q_j$ En términos de una matriz $K_{ij}(q_k)$ que es en principio una función de las coordenadas. En otras palabas, estamos estudiando sistemas de la forma general $K(\dot q_i, q_i)=\frac 12 K_{12}(q_k)\,\dot q_1\dot q_2+\frac 12 K_{21}(q_k)\,\dot q_2\dot q_1+\frac 12 K_{11}(q_k)\,\dot q_1^2+\dots$ Las ecuaciones de movimiento de este sistema se escriben como $\frac{d}{dt}\left( \frac{\partial L}{\partial \dot q_i}\right)-\frac{\partial L}{\partial q_i}=0$ o en otras palabras $\frac{d}{dt}{\left(K_{ij}(q_k)\dot q_j\right)}-\frac{\partial V(q_k)}{\partial q_i}-\frac12\frac{\partial K_{jk}}{\partial q_i}\dot q_j\dot q_k=0$ Este sistema tiene una solución estática $q_i=q_i^0$ si el potencial tiene un punto estacionario, es decir si $\frac{\partial V(q_k^0)}{\partial q_i}=0$ En este punto se cumple que $\frac{d\left(K_{ij}(q_k)\dot q_j^0\right)}{dt}-\frac12\frac{\partial K_{jk}}{\partial q_i}\dot q_j^0\dot q_k^0=0$ Lo que se resuelve inmediatamente con $\dot q_k^0=0$ Si ahora perturbamos el sistema sacandolo del punto estacionario con una pequeña variación de las coordenadas $\delta q_i$, tenemos $q_k=q_k^0+\delta q_k$ Lo que en la energía cinética nos permite escribir $K(\dot {\delta q_k}, q_k^0+\delta q_k)=\frac 12 K_{ij}(q_k^0+\delta q_k)\,(\dot q_i^0+\dot{\delta q_i})(\dot q_j^0+\dot{\delta q_j})=\frac 12 K_{ij}(q_k^0+\delta q_k)\,\dot{\delta q_i}\dot{\delta q_j}$ $=\frac 12 K_{ij}(q_k^0)\,\dot{\delta q_i}\dot{\delta q_j}+{\cal O(\delta q_k)^3}=\frac12m_{ij}\dot{\delta q_i}\dot{\delta q_j}$ Donde en la úlitma igualdad omitimos los órdener superiores y definimos la *matriz de masas* $m_{ij}=K_{ij}(q_k^0)$. Por otro lado en el potencial $V(q_i^0+\delta q_i)=V(q_k^0)+\frac{\partial V(q_k^0)}{\partial q_i}\delta q_i+\frac 12 \frac{\partial^2V(q_k^0)}{\partial q_i\partial q_j} \delta q_i\delta q_j+{\cal O}(\delta q_k^3)$ De nuevo, el término lineal se va y el término constante no contribuye a las ecuaciones de movimiento por lo que lo podemos omitir, y tenemos $V(q_i^0+\delta q_i)=\frac 12 k_{ij} \delta q_i\delta q_j$ Donde la *matriz de restauración* es $k_{ij}=\frac{\partial^2V(q_k^0)}{\partial q_i\partial q_j}$. Con esto el lagrngiano se lee $L =\frac 12 m_{ij}\,\dot{\delta q_i}\dot{\delta q_j}-\frac 12 k_{ij} \delta q_i\delta q_j$ De donde se obtienen inmediatamente las ecuaciones de movimiento $m_{ij}\ddot{\delta q}_j+k_{ij}\delta q_j=0$ Insertando en Ansatz $\delta q_i=c_ie^{i\omega \,t}$ $\left(k_{ij}-\omega^2 m_{ij}\right)c_j =0$ O, en notación matricial $\left(k-\omega^2m\right)\cdot\vec c=0$ Esto es una ecuación de autovalores, la cual tiene una solución no trivial siempre que el determinante se anule ${\sf Det}\left(k-\omega^2m\right)=0$ Si tenemos $N$ grados de libertad $q_i$, entonces la matriz es de $N\times N$. Esto implica que el determinante será un polinomio de orden $N$ en los elementos de la matriz, y por lo tanto es un polinomio de orden $N$ en $\omega^2$. Las raíces de este polinomio nos darán los posibles valores de $\omega^2$, que serían en principio $N$ valores diferentes $\omega^2_i$ con $i\in\{1\dots N\}$. Çon cada uno de estos valores, deberíamos obtener el autovector correspondiente según $\left(k-\omega^2_im\right)\cdot \vec c_i=0$ En principio hay $N$ vectores diferentes $\vec c_i$ con $i\in\{1\dots N\}$. Nótese que cada uno de ellos tiene $N$ componentes $c_{ij}$ con $j\in\{1\dots N\}$. Se puede probar que estos vectores son reales, y lo asumiremos en lo que sige. Si multimplicamos por $\vec c_j^t$ la ecuación para $\vec c_i$ tenemos $\vec c_j^t\cdot k\cdot\vec c_i=\omega^2_i\,\,\vec c_j^t\cdot m\cdot\vec c_i$ Si en cambio multiplicamos por $\vec c_i^t$ la ecuación para $\vec c_j$ nos queda $\vec c_i^t\cdot k\cdot\vec c_j=\omega^2_j\,\,\vec c_i^t\cdot m\cdot\vec c_j$ Transponiendo la segunda ecuación y restandola de la primera $\left(\omega_j^2-\omega_i^2\right)\,\,\vec c_i^t\cdot m\cdot\vec c_j=0$ Con lo que tenemos que cuando $i\neq j$ se cumple que $\vec c_i^t\cdot m\cdot\vec c_j=0$ Esta ecuación no nos dice nada del caso $i=j$, pero dado que los vectores $\vec c_i$ están determinados a menos de una constante multiplicativa, podemos definir $\vec c_i^t\cdot m\cdot\vec c_i=1$ Lo que se puede resumir como $\vec c_i^t\cdot m\cdot\vec c_j=\delta_{ij}$ Esto a su vez implica, usando la expresión de más arriba, que $\vec c_i^t\cdot k\cdot\vec c_j=\omega^2_j\,\delta_{ij}$ Si en cambio tomammos la ecuación que habíamos escrito más arriba, y ponemos $i=j$ en ella $\vec c_i^t\cdot k\cdot\vec c_i=\omega^2_i\,\,\vec c_i^t\cdot m\cdot\vec c_i$ podemos despejar $\omega^2_i=\frac{\vec c_i^t\cdot k\cdot \vec c_i}{\vec c_i^\dagger\cdot m\cdot \vec c_i}$ Con lo que vemos que el signo de $\omega^2$ está dado por el signo de $\vec c_i^\dagger\cdot k\cdot \vec c_i$ y de $\vec c_i^\dagger\cdot m\cdot \vec c_i$. La primera expresión representa la variación del potencial cuando nos apartamos del punto estacionario una cantidad $\delta q_j=c_{ij}$. Por lo tanto será positivo si el punto estacionario es un mínimo, y negativo en caso contrario. La segunda expresión representa la energía cinética de una perturbación con velocidad $\dot{\delta q}_j=c_{ij}$, y por lo tanto debe ser positiva. La solución general del problema se puede escribir como $\delta q_j=\Re\big{(}\underbrace{\left(A_i^+ \,e^{+i\,\omega_i\,t}+A_i^- \,e^{-i\,\omega_i\,t}\right)}_{\delta u_i}c_{ij}\big{)}$ Con lo que podemos escribir los modos normales según $\delta q_j=c_{ij} \delta u_i$ o en términos matriciales $\vec{\delta q}=\vec c_i\delta u_i$ Reemplazando en el lagrangiano $L =\frac 12 \dot{\vec {\delta q}}^t\cdot m\cdot\dot{\vec {\delta q}}-\frac 12 \vec {\delta q}^t\cdot k\cdot \vec {\delta q}=\frac12\dot{\delta u}_i\,\,\vec c_i^t\cdot m\cdot\vec c_j\,\,\dot{\delta u}_j-\frac12\delta u_i\,\,\vec c_i^t\cdot k\cdot\vec c_j\,\,\delta u_j$ En el primer término podemos usar la relación de ortogonalidad que habíamos obtenido antes $\vec c_i^2\cdot m\cdot\vec c_j=\delta_{ij}$ mientras que en el segundo término usamos la ecuación de autovalores $\vec c_i^t\cdot k\cdot\vec c_j=\omega^2_j\,\delta_{ij}$. Esto nos deja con $L=\sum_i\frac12\left( \dot{\delta u}_i^2-\omega_i^2\delta u_i^2\right)$ Donde por claridad escribimos explícitamente la suma en $i$. El sistema se ha descompuesto en un conjunto de $N$ osciladores armónicos desacoplados, con las frecuencias normales. #### Caso general Supongamos ahora un lagrangiano general $L(\dot q_i,q_i,t)$. Sus ecuaciones de movimiento serán $\frac d{dt}\left(\frac{\partial L}{\partial \dot q_i}\right)-\frac{\partial L}{\partial q_i}=0$ Supongamos que tenemos una solución estática de estas ecuaciones $q_i=q_i^0$, entonces se cumple que $\frac{\partial^2 L}{\partial t\partial \dot q_i}(0,q_i^0,t)-\frac{\partial L}{\partial q_i}(0,q_i^0,t)=0$ Como vimos en el caso unidimensional más arriiba, esta condición es análoga a la condición de punto estacionario para este caso más general. Si ahora perturbamos la solución $q_i=q_i^0+\delta q_i$ y reemplazamos en $L$ $L=L_0+\frac{\partial L}{\partial q_i}\delta q_i+\frac{\partial L}{\partial \dot q_i}\dot{\delta q_i}+\frac12\left(\frac{\partial^2 L}{\partial q_i\partial q_j}\delta q_i\delta q_j+\frac{\partial^2 L}{\partial \dot q_i\partial \dot q_j}\dot{\delta q}_i\dot{\delta q}_j+2\frac{\partial^2 L}{\partial q_i\partial \dot q_j}\delta q_i\dot{\delta q}_j\right)$ De nuevo, los primeros tres términos no van a contribuir a las ecuaciones de movimiento, que se escriben $\frac d{dt}\left( \frac{\partial^2 L}{\partial \dot q_i\partial \dot q_j}\dot{\delta q}_j+\frac{\partial^2 L}{\partial q_j\partial \dot q_i}\delta q_j \right)-\left(\frac{\partial^2 L}{\partial q_i\partial q_j} \delta q_j+\frac{\partial^2 L}{\partial q_i\partial \dot q_j} \dot{\delta q}_j\right)=0$ O, reordenando $\frac d{dt}\big{(} \underbrace{\frac{\partial^2 L}{\partial \dot q_i\partial \dot q_j}}_{m_{ij}(t)}\dot{\delta q}_j\big{)}+\underbrace{\left(\frac d{dt}\left(\frac{\partial^2 L}{\partial q_j\partial \dot q_i} \right)- \frac{\partial^2 L}{\partial q_i\partial q_j} \right)}_{k_{ij}(t)}\delta q_j=0$ Lo que queda escrito como $\frac d{dt}\left(m_{ij}(t)\frac{d{\delta q}_j}{dt}\right)+k_{ij}(t)\delta q_j=0$ Esto es un conjunto de problemas de Sturm-Liuville acoplados. En general no es fácil desacoplar esos sitemas para encontrar una solución, por lo que se estudian con tecnicas numéricas. > Nota: hasta este punto, todas las cuentas de esta sección son igualmente válidas incluso si la solución que estamos perturbando no es estática. En el caso particular de un lagrangiano que no dependa del tiempo, recuperamos la ecuación $m_{ij}\ddot{\delta q}_j+k_{ij}\delta q_j=0$ A partir de la cual trabajamos en la sección anterior. Un detalle a tener en cuenta es que ahora la matriz $m$ no tiene por qué ser definida positiva. Por lo tanto en la expresión $\omega^2_i=\frac{\vec c_i^t\cdot k\cdot\vec c_i}{\vec c_i^t\cdot m\cdot\vec c_i}$ Ahora pueden aparecer, además de las inestabilidades originadas en el signo negativo del numerador (las llamadas *taquiónicas*), otras inestabilidades originadas en un signo negativo en el denominador (o *por fantasmas*).